
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 ![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,S△ABC=8![]() ,点M,P,N分别是边AB,BC,AC上任意一点,则:
,点M,P,N分别是边AB,BC,AC上任意一点,则:
(1)AB的长为____________.
(2)PM+PN的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
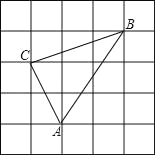
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为 ![]() ,宽为
,宽为 ![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出 ![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若 ![]() ,
,![]() ,则
,则 ![]() ;
;
(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式![]() .在图形上把每一部分的面积标写清楚.
.在图形上把每一部分的面积标写清楚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣![]() x+m交折线OAB于点E.
x+m交折线OAB于点E.
(1)请写出m的取值范围 ;
(2)记△ODE的面积为S,求S与m的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
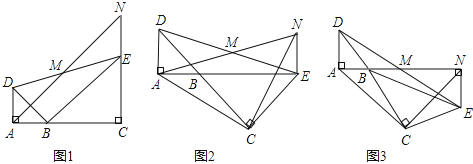
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com