
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
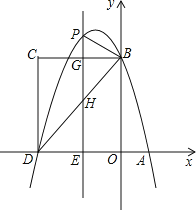
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4;(2)PG=﹣
x+4;(2)PG=﹣![]() m2﹣
m2﹣![]() m;(3)﹣1或﹣
m;(3)﹣1或﹣![]() .
.
【解析】
试题分析:(1)将点A和点B的坐标代入求出函数解析式;(2)根据点E的坐标得出点P的坐标,根据点B和点E的坐标得出点G的坐标,然后根据PG=PE件EG得出;(3)首先根据△BGP和△DEH相似得出EH的长度,然后根据△BGP∽△DEH和△PGB∽△DEH两种情况求出m的值.
试题解析:(1)∵抛物线y=﹣![]() x2+bx+c与x轴交于点A(1,0),与y轴交于点B(0,4),
x2+bx+c与x轴交于点A(1,0),与y轴交于点B(0,4),
∴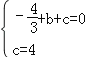 解得
解得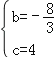 ∴抛物线的解析式为y=﹣
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+4
x+4
(2)∵E(m,0),B(0,4),PE⊥x轴交抛物线于点P,交BC于点G,
∴P(m,﹣![]() m2﹣
m2﹣![]() m+4),G(m,4),∴PG=﹣
m+4),G(m,4),∴PG=﹣![]() m2﹣
m2﹣![]() m+4﹣4=﹣
m+4﹣4=﹣![]() m2﹣
m2﹣![]() m;
m;
(3)由﹣![]() x2﹣
x2﹣![]() x+4=0,解得x=1或﹣3,∴D(﹣3,0).
x+4=0,解得x=1或﹣3,∴D(﹣3,0).
当点P在直线BC上方时,﹣![]() x2﹣
x2﹣![]() x+4=4,得﹣2<m<0.
x+4=4,得﹣2<m<0.
∵△BGP∽△DEH,∴![]() ,即
,即![]()
在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似分两种情况:
①如果△BGP∽△DEH,那么![]() =
=![]() ,即
,即 ![]() =
=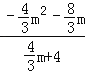 ,解得m=﹣1;
,解得m=﹣1;
②如果△PGB∽△DEH,那么![]() =
=![]() ,即
,即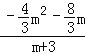 =
=![]() ,得m=﹣
,得m=﹣![]() .
.
综上所述,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
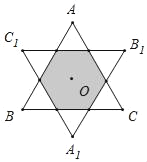
【题目】如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
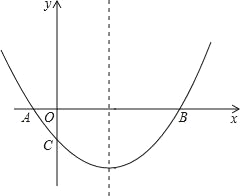
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0, ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某冷库一天的冷冻食品进出记录如下表![]() 运进用正数表示,运出用负数表示
运进用正数表示,运出用负数表示![]() :
:
进出数量 |
| 4 |
| 2 |
|
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由.
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元.
方案二:不管运进还是运出每吨冷冻食品费用都是600元.从节约运费的角度考虑,选用哪一种方案比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足![]() ,
,![]() ,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒
,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒![]() 个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.

(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)在![]() 的条件下,当P、Q两点间的距离是6个单位长度时,求OP的长.
的条件下,当P、Q两点间的距离是6个单位长度时,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.

(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是 cm/s; 点B运动的速度是 cm/s.
②若点P为直线l上一点,且PA﹣PB=OP,求![]() 的值;
的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的门票销售分两类:一类为散客门票,价格为![]() 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票![]() 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打![]() 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游![]() 人,购买门票需要
人,购买门票需要![]() 元
元
(1)如果每人分别买票,求![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:
(2)如果购买团体票,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(3)请根据人数变化设计一种比较省钱的购票方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com