
【题目】如图,点![]() 是正方形
是正方形![]() 边
边![]() 上一点,连接
上一点,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 手点
手点![]() ,连接
,连接![]() .
.
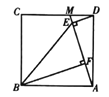
(1)求证:![]() ;
;
(2已知![]() ,四边形
,四边形![]() 的面积为24,求
的面积为24,求![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]()
![]() .
.
【解析】(1)通过证明△ABF≌△DEA得到BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到![]() xx+
xx+![]() x2=24,解方程求出x得到AE=BF=6,则EF=x-2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
x2=24,解方程求出x得到AE=BF=6,则EF=x-2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
详(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DEA中
 ,
,
∴△ABF≌△DEA(AAS),
∴BF=AE;
(2)解:设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴![]() xx+
xx+![]() x2=24,解得x1=6,x2=-8(舍去),
x2=24,解得x1=6,x2=-8(舍去),
∴EF=x-2=4,
在Rt△BEF中,BE=![]() ,
,
∴sin∠EBF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
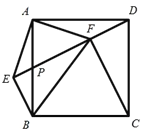
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为1,点
的边长为1,点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上将正方形
轴的负半轴上将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至正方形
至正方形![]() 的位置,
的位置,![]() 与
与![]() 相交于点
相交于点![]() ,则
,则![]() 的坐标为____________.
的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
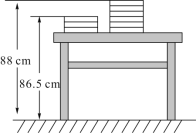
【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 和点
和点![]() 是线段
是线段![]() 的两个端点,线段
的两个端点,线段![]() ,点
,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,点
的对称中心,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点![]() 是点
是点![]() 和点
和点![]() 的对称中心.(
的对称中心.(![]() 为正整数)
为正整数)
![]()
(1)填空:线段![]() ____________ ;线段
____________ ;线段![]() _____________ (用含
_____________ (用含![]() 的最简代数式表示)
的最简代数式表示)
(2)试写出线段![]() 的长度(用含
的长度(用含![]() 和
和![]() 的代数式表示,无需说明理由)
的代数式表示,无需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )
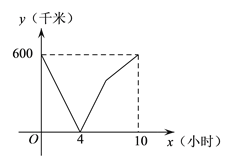
A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
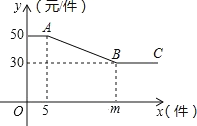
【题目】某商店经销某种玩具,该玩具每个进价 20 元,为进行促销,商店制定如下“优惠” 方案:如果一次销售数量不超过 5 个,则每个按 50 元销售:如果一次销售数量超过 5 个,则每增加一个,所有玩具均降低 1 元销售,但单价不得低于 30 元,一次销售该玩具的单价 y(元)与销售数量 x(个)之间的函数关系如下图所示.
(1)结合图形,求出 m 的值;射线 BC 所表示的实际意义是什么;
(2)求线段 AB 满足的 y 与 x 之间的函数解析式,并直接写出自变量的取值范围;
(3)当销售 15 个时,商店的利润是多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com