Question

19．阅读以下材料：
对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M$\left\{{-1，2，3}\right\}=\frac{-1+2+3}{3}=\frac{4}{3}$；min{-1，2，3}=-1；min$\left\{{-1，2，a}\right\}=\left\{\begin{array}{l}a\;\;\;\;\;\;\;\;（a≤-1）\\-1\;\;\;\;\;\;\;（a＞-1）.\end{array}$
解决下列问题：
（1）填空：min{sin30°，cos45°，tan30°}=sin30°；
（2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x；
②根据①，你发现了结论：
“如果M{a，b，c}=min{a，b，c}，那么a=b=c（填a，b，c的大小关系）”．
③运用②的结论，填空：
若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=-4．
（3）填空：min{x+1，（x-1）²，2-x}的最大值为1．

Answer 1

分析 （1）因为用min（a，b，c）表示这三个数中最小的数．分别计算sin30°，cos45°，tan30°的值，比较得出答案即可；
（2）①结合题意，分情况讨论，将实际问题与数学思想联系起来，读懂题列出算式或一元一次不等式组即可求解；
②类比直接得出结论即可；
③利用②的结论得出2x+y+2=2x-y，则y=-1，x+2y=2x-y，得出x=-3，进一步计算x+y=-4；
（3）建立函数则y=x+1，y=（x-1）²，y=2-x作出三个函数的图象，利用图象解题．

解答 解：（1）∵sin30°=$\frac{1}{2}$，cos45°=$\frac{\sqrt{2}}{2}$，tan30°=$\frac{\sqrt{3}}{3}$，
∴min{sin30°，cos45°，tan30°}=sin30°；
（2）①∵M{2，x+1，2x}=$\frac{2+x+1+2x}{3}$═x+1=min{2，x+1，2x}，
∴$\left\{\begin{array}{l}{2≥x+1}\\{2x≥x+1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x≤1}\\{x≥1}\end{array}\right.$，
∴x=1．
②∵M{{a，b，c}}=$\frac{a+b+c}{3}$，如果min{a，b，c}=c，则a≥c，b≥c．则有$\frac{a+b+c}{3}$=c，
即a+b-2c=0．
∴（a-c）+（b-c）=0．
又a-c≥0，b-c≥0．
∴a-c=0且b-c=0．
∴a=b=c．
其他情况同理可证，故a=b=c．
③∵2x+y+2=x+2y=2x-y，
∴2x+y+2=2x-y，则y=-1，
∴x+2y=2x-y，得出x=-3，
∴x+y=-4；

（3）作出y=x+1，y=（x-1）²，y=2-x的图象．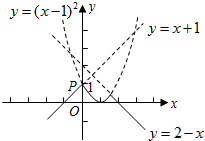

由图可知min{x+1，（x-1）²，2-x}的最大值为1．
故答案为：sin30°，a=b=c，-4，1．

点评 本题考查了一次函数、二次函数的图象与性质，比较大小以及利用已知提供信息得出函数值的方法，此题综合性较强，读懂题目信息并理解新定义“M”与“min”的意义是解题的关键．