
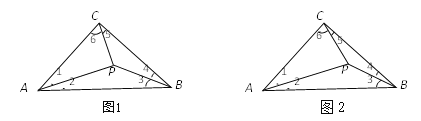
【题目】如图1,已知:在△ABC中,∠ACB=90°,AC=BC,△ABC内一点P将三个内角分成6个角(即∠1、∠2、∠3、∠4、∠5、∠6).
(1)若∠1=∠3=∠5,求![]() 的值;
的值;
(2)如图2,已知:AP=AC.
①若PB=PC,求证:∠1=2∠4;
②若∠1=30°,求证:PB=PC.
【答案】(1)2:5;(2)①证明见解析;②证明见解析.
【解析】试题分析:(1)根据题意可知∠APC=90°,然后根据相似三角形的判定与性质,结合勾股定理可求解;
(2)①根据等腰三角形的等边对等角,结合三角形的内角和定理可证明;
②过P作PD⊥AC于D,PE⊥BC于E, 易得四边形PDCE为矩形,然后根据30°角的直角三角形和线段的垂直平分线的性质可求解.
试题解析:(1)∵AC=BC ∠ACB=90°, ∴∠CAB=∠ABC=45°.
∵∠1=∠3=∠5 , ∴∠2=∠4 ,∴∠APB=180°-(∠2+∠3)=180°-45°=135°,
同理,∠BPC=135°. ∴∠APC=90°
设AC=a,PC=x,则![]() ,易证:△APB∽△BPC,∴
,易证:△APB∽△BPC,∴![]() ,
,
∴![]() ,
, ![]() ,在Rt△PAC中,
,在Rt△PAC中, ![]() ;∴
;∴![]()
∵![]() ,
, ![]() ,
,
∴![]() ;
;
(2)①∵PB=PC,则∠4=∠5,设∠4=∠5=![]() ,
,
∵AP=AC,则∠6=∠APC=90°![]() ,即∠1=180°-2(90°
,即∠1=180°-2(90°![]() )=2
)=2![]() ,
,
即∠1=2∠4;

②如图所示,过P作PD⊥AC于D,PE⊥BC于E,
易得四边形PDCE为矩形,
在直角△APD中,∠1=30°,∴PD=![]() PA,
PA,
又AP=AC=BC,∴PD=CE=![]() BC,即PF垂直平分BC,
BC,即PF垂直平分BC,
∴PB=PC.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①所有的正三角形都相似;
②所有的正方形都相似;
③所有的等腰直角三角形都相似;
④所有的矩形都相似;⑤所有的菱形都相似.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a、b、c满足 ![]() 求:
求:
(1)a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
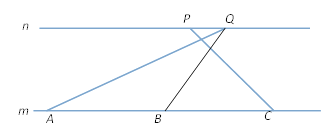
【题目】如图,河的两岸![]() 与
与![]() 互相平行,A、B、C是
互相平行,A、B、C是![]() 上的三点,P、Q是
上的三点,P、Q是![]() 上的两点.在A处测得∠QAB=30°,在B处测得∠QBC=60°,在C处测得∠PCB=45°,已知AB=BC=20米,求PQ的长(结果保留根号).
上的两点.在A处测得∠QAB=30°,在B处测得∠QBC=60°,在C处测得∠PCB=45°,已知AB=BC=20米,求PQ的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之“有限小数或无限循环小数均可化为分数”.
例如: ![]()
![]()
![]()
反之![]()
![]()
那么![]() 怎么化成
怎么化成![]() 呢?
呢?
解:∵![]()
∴不妨设![]() ,则上式变为10x=3+x,解得x=
,则上式变为10x=3+x,解得x=![]() 即
即![]() .
.
根据以上材料,回答下列问题:
(1)将分数化为小数: ![]() =_________,
=_________,![]() =_________;
=_________;
(2)将小数化为分数: ![]() =_________,
=_________,![]() =_________;
=_________;
(3)将小数![]()
![]() 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com