

分析 (1)先证明△ABQ≌△CAP,从而得到∠BAQ=∠ACP,然后利用三角形的外角的性质求解即可;
(2)设时间为t,则AP=BQ=t,PB=6-t,①当∠PQB=90°时,②当∠BPQ=90°时,列方程得到结果;
(3)先证明△ACQ≌△CBP,从而得到∠CAQ=∠BCP然后依据∠CAM+∠ACM=∠BCP+∠ACM求解即可.
解答 (1)证明:∵等边三角形中,AB=AC,∠B=∠CAP=60°
又由条件得AP=BQ,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;
(2)解:设时间为t,则AP=BQ=t,PB=6-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得6-t=2t,t=2;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(6-t),t=4;
∴当第2秒或第4秒时,△PBQ为直角三角形;
(3)解:∵在等边三角形中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,
又由条件得BP=CQ,AC=BC
∴△PBC≌△QCA(SAS),
∴∠BPC=∠MQC,
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=180°-60°=120°.
点评 本题考查等边三角形的性质、全等三角形的判定与性质,掌握等边三角形的性质、全等三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:解答题
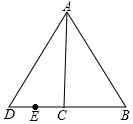 如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | … | -0.0001 | 0 | 0.0001 | 1 | 1000 | … |
| $\root{3}{a}$ | … | -0.1 | 0 | 1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.
如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com