
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.
(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

【答案】(1)![]() (2)(-6,0)或(-2,0).
(2)(-6,0)或(-2,0).
【解析】分析:(1)把A点坐标代入直线解析式可求得m的值,则可求得A点坐标,再把A点坐标代入双曲线解析式可求得k的值,可求得双曲线解析式;
(2)设P(t,0),则可表示出PC的长,进一步表示出△ACP的面积,可得到关于t的方程,则可求得P点坐标.
详解:(1)把A点坐标代入y=![]() x+2,可得:3=
x+2,可得:3=![]() m+2,解得:m=2,∴A(2,3).∵A点也在双曲线上,∴k=2×3=6,∴双曲线解析式为y=
m+2,解得:m=2,∴A(2,3).∵A点也在双曲线上,∴k=2×3=6,∴双曲线解析式为y=![]() ;
;
(2)在y=![]() x+2中,令y=0可求得:x=﹣4,∴C(﹣4,0).∵点P在x轴上,∴可设P点坐标为(t,0),∴CP=|t+4|,且A(2,3),∴S△ACP=
x+2中,令y=0可求得:x=﹣4,∴C(﹣4,0).∵点P在x轴上,∴可设P点坐标为(t,0),∴CP=|t+4|,且A(2,3),∴S△ACP=![]() ×3|t+4|.∵△ACP的面积为3,∴
×3|t+4|.∵△ACP的面积为3,∴![]() ×3|t+4|=3,解得:t=﹣6或t=﹣2,∴P点坐标为(﹣6,0)或(﹣2,0).
×3|t+4|=3,解得:t=﹣6或t=﹣2,∴P点坐标为(﹣6,0)或(﹣2,0).


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
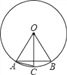
A. 弦AB的长等于圆内接正六边形的边长
B. 弦AC的长等于圆内接正十二边形的边长
C. ![]()
D. ∠BAC=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE,若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为( )
的值为( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城镇在对一项工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲队工程款2万元,付乙队工程款1.5万元.现有三种施工方案:(![]() )由甲队单独完成这项工程,恰好如期完工;(
)由甲队单独完成这项工程,恰好如期完工;(![]() )由乙队单独完成这项工程,比规定工期多6天;(
)由乙队单独完成这项工程,比规定工期多6天;(![]() )由甲乙两队
)由甲乙两队![]() 后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为
后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为![]() 天,依题意列出方程:
天,依题意列出方程:![]() .
.
(1)请将(![]() )中被墨水污染的部分补充出来:________;
)中被墨水污染的部分补充出来:________;
(2)你认为三种施工方案中,哪种方案既能如期完工,又节省工程款?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时,点
移动,同时,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,已知点
的延长线移动,已知点![]() 、
、![]() 的移动速度相同,
的移动速度相同,![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
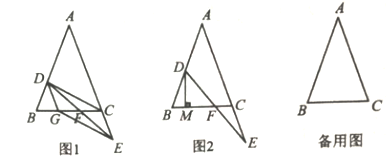
(1)如图1,当点![]() 在线段
在线段![]() 上时,过点
上时,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:点
,求证:点![]() 是
是![]() 的中点;
的中点;
(2)如图2,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当点
,当点![]() 、
、![]() 在移动过程中,线段
在移动过程中,线段![]() 、
、![]() 、
、![]() 有何数量关系?请直接写出你的结论: .
有何数量关系?请直接写出你的结论: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC三边的长分别为AB=m2﹣n2,AC=2mn,BC=m2+n2,其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3,那么S1、S2、S3之间的数量关系为_____.
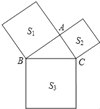
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.
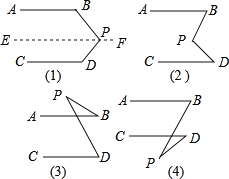
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
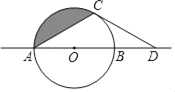
【题目】如图,⊙O半径为1,AB是⊙O的直径,C是⊙O上一点,连接AC,⊙O外的一点D 在直线AB上.
(1)若AC=![]() ,OB=BD.
,OB=BD.
①求证:CD是⊙O的切线.
②阴影部分的面积是 .(结果保留π)
(2)当点C在⊙O上运动时,若CD是⊙O的切线,探究∠CDO与∠OAC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com