
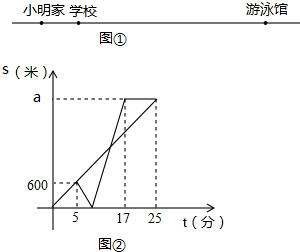
 图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.
图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.分析 (1)根据时间、路程和速度关系得出小亮的速度,进而得出全路程即可;
(2)根据路程和时间的关系得出小明骑自行车时s与t之间的函数关系式即可;
(3)根据几种情况得出小明和小亮相距900米时t的值即可.
解答 解:(1)由图象可得:小亮的速度为:600÷5=120米/分钟;
可得a的值为:25×120=3000米;
故答案为:120;3000;
(2)因为小明骑自行车的速度始终不变,所以可得其速度为:(600+3000)÷(17-5)=300米/分钟;
所以可得小明骑自行车时s与t之间的函数关系式为:s=300t;
(3)当小明回家的途中与小亮相距900米,可得:900=(120+120)t,
解得:t=$\frac{15}{4}$分;
当小明从家回来时,小亮比小明多900米,可得:120t+600-300(t-5)=900,
解得:t=$\frac{20}{3}$分;
当从家回来时,小明比小亮多900米,可得:120t+900+600=300(t-5),
解得:t=$\frac{50}{3}$分;
小明到达游泳馆后,小亮与小明相距900米时,时间为17.5分;
综上所述小明和小亮相距900米时t的值为$\frac{15}{4}$,$\frac{20}{3}$,$\frac{50}{3}$,17.5分.
点评 此题考查一次函数问题,解题的关键是先根据速度、时间、路程之间关系求出速度.


科目:初中数学 来源: 题型:填空题
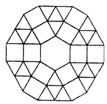 如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.
如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
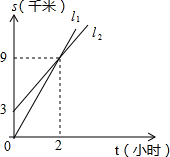 A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:
A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
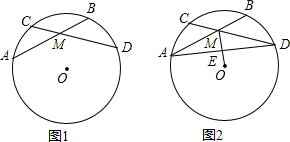
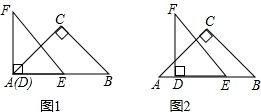 如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )| A. |  | B. | 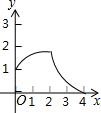 | C. | 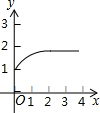 | D. | 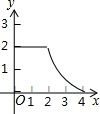 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
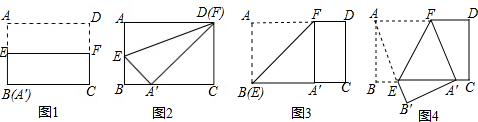
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )
如图所示,在Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )| A. | AC=AE=BE | B. | AD=BD | C. | AC=BD | D. | CD=DE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com