
【题目】如图,已知正方形纸片ABCD的边长为2,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
(1)观察操作结果,找到一个与△EDP相似的三角形,并证明你的结论;
(2)当点P位于CD中点时,你找到的三角形与△EDP周长的比是多少?
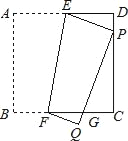
【答案】(1)与△EDP相似的三角形是△PCG.证明见解析;(2)4:3.
【解析】分析:(1)根据题意,∠EPG=90°,可得∠EPD+∠CPG=90°,又∠EPD+∠PED=90°,所以∠CPG=∠PED.加上∠C=∠D,可得△EDP∽△PCG;
(2)根据相似三角形性质求解.因为CP=1,所以需求对应边DE的长度.设DE=x,则AE=EP=2-x,根据勾股定理可求.
详解:(1)与△EDP相似的三角形是△PCG.
证明:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°.
由折叠知∠EPQ=∠A=90°.
∴∠1+∠3=90°,∠1+∠2=90°.
∴∠2=∠3.
∴△PCG∽△EDP.
(2)设ED=x,则AE=2﹣x,
由折叠可知:EP=AE=2﹣x.
∵点P是CD中点,
∴DP=1.
∵∠D=90°,
∴ED2+DP2=EP2,
即x2+12=(2﹣x)2
解得x=![]() .
.
∴![]() .
.
∵△PCG∽△EDP,
∴![]() .
.
∴△PCG与△EDP周长的比为4:3.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】近年来,德强学校初中部中考屡创佳绩,捷报频传.为了吸纳更多的优质生源,学校决定要新建一栋![]() 层的教学大楼,每层楼有
层的教学大楼,每层楼有![]() 间教室,进出这栋大楼共有
间教室,进出这栋大楼共有![]() 道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对
道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对![]() 道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,
道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,![]() 分钟可以通过
分钟可以通过![]() 名学生;当同时开启一道正门和一道侧门时
名学生;当同时开启一道正门和一道侧门时![]() 分钟可以通过
分钟可以通过![]() 名学生.
名学生.
(1)正常情况下,平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低![]() ,安全检查规定,在紧急情况下全大楼的学生应在
,安全检查规定,在紧急情况下全大楼的学生应在![]() 分钟内通过这
分钟内通过这![]() 道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这
道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这![]() 道门是否符合安全规定?请说明理由.
道门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
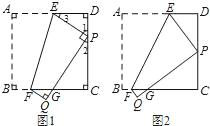
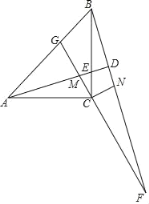
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点E是BC上一点(不与点B,C重合),点M是AE上一点(不与点A,E重合),连接并延长CM交AB于点G,将线段CM绕点C按顺时针方向旋转90°,得到线段CN,射线BN分别交AE的延长线和GC的延长线于D,F.
(1)求证:△ACM≌△BCN;
(2)求∠BDA的度数;
(3)若∠EAC=15°,∠ACM=60°,AC=![]() +1,求线段AM的长.
+1,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店正在开展“感恩十年,童行有你”促销活动一次性购物不超过![]() 元不享受优惠;一次性购物超过
元不享受优惠;一次性购物超过![]() 元但不超过
元但不超过![]() 元,超过
元,超过![]() 元的部分九折优惠;一次性购物超过
元的部分九折优惠;一次性购物超过![]() 元一律八折.在活动期间,张三两次购物分别付款
元一律八折.在活动期间,张三两次购物分别付款![]() 元、
元、![]() 元,若张三选择这两次购物合并成一次性付款可以节省___________元.
元,若张三选择这两次购物合并成一次性付款可以节省___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
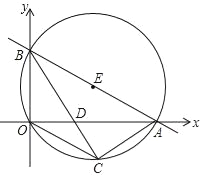
【题目】直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
(1)求A、B、C三点坐标;
(2)求经过O、C、A三点的抛物线解析式;
(3)直线AB上是否存在点P,使得△COP的周长最小?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 、
、![]() 三地依次在同一直线上,
三地依次在同一直线上,![]() ,
,![]() 两地相距
两地相距![]() 千米,甲、乙两车分别从
千米,甲、乙两车分别从![]() ,
,![]() 两地同时出发,相向匀速行驶。行驶
两地同时出发,相向匀速行驶。行驶![]() 小时两车相遇,再经过
小时两车相遇,再经过![]() 小时,甲车到达
小时,甲车到达![]() 地,然后立即调头,并将速度提高
地,然后立即调头,并将速度提高![]() 后与乙车同向行驶,经过一段时间后两车同时到达
后与乙车同向行驶,经过一段时间后两车同时到达![]() 地,则
地,则![]() ,
,![]() 两地相距_____________千米.
两地相距_____________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com