
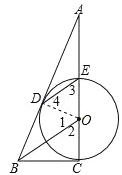
【题目】如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.

(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO=![]() ,求AO的长.
,求AO的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连接OD,由DE∥BO,得到∠1=∠4,∠2=∠3,通过证明△DOB≌△COB,得到∠OCB=∠ODB,问题得证;
(2)根据三角函数tan∠DEO=tan∠2=![]() ,设OC=r,BC=
,设OC=r,BC=![]() r,得到BD=BC=
r,得到BD=BC=![]() r,由切割线定理得到AD=2
r,由切割线定理得到AD=2![]() ,再根据平行线分线段成比例得到比例式即可求得结果.
,再根据平行线分线段成比例得到比例式即可求得结果.
试题解析:(1)连接OD,
∵DE∥BO,
∴∠1=∠4,∠2=∠3,
∵OD=OE,
∴∠3=∠4,
∴∠1=∠2,
在△DOB与△COB中,
 ,
,
∴△DOB≌△COB,
∴∠OCB=∠ODB,
∵BD切⊙O于点D,
∴∠ODB=90°,
∴∠OCB=90°,
∴AC⊥BC,
∴直线BC是⊙O的切线;
(2)∵∠DEO=∠2,
∴tan∠DEO=tan∠2=![]() ,
,
设OC=r,BC=![]() r,
r,
由(1)证得△DOB≌△COB,
∴BD=BC=![]() r,
r,
由切割线定理得:AD2=AEAC=2(2+r),
∴AD=2![]() ,
,
∵DE∥BO,
∴![]() ,
,
∴![]() ,
,
∴r=1,
∴AO=3.


科目:初中数学 来源: 题型:
【题目】由二次函数y=2(x﹣3)2+1可知( )
A.其图象的开口向下
B.其图象的对称轴为x=﹣3
C.其最大值为1
D.当x<3时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
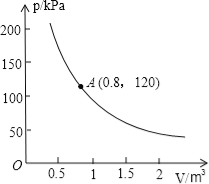
(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全起见,气体的体积应不大于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护水资源,人人有责,我国是缺水国家,目前可利用淡水资源总量仅约为899000亿立方米,899000亿用科学记数法表示为( )
A.8.99×1013 B.0.899×1014 C.8.99×1012 D.89.9×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=2x2向上平移1个单位,再向右平移2个单位,则平移后的抛物线为( )
A.y=2(x+2)2+1 B.y=2(x﹣2)2+1
C.y=2(x+2)2﹣1 D.y=2(x﹣2)2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com