
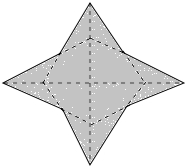
 如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是6$\sqrt{3}$-6.
如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是6$\sqrt{3}$-6. 分析 根据菱形的性质以及AB=2,∠BAD=60°,可得出线段AO和BO的长度,同理找出A′O、D′O的长度,结合线段间的关系可得出AD′的长度,通过角的计算得出∠AED′=30°=∠EAD′,即找出D′E=AD′,再通过解直角三角形得出线段EF的长度,利用分割图形法结合三角形的面积公式以及菱形的面积公式即可求出阴影部分的面积.
解答 解:在图中标上字母,令AB与A′D′的交点为点E,过E作EF⊥AC于点F,如图所示.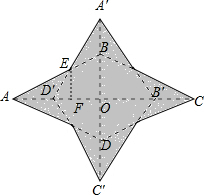
∵四边形ABCD为菱形,AB=2,∠BAD=60°,
∴∠BAO=30°,∠AOB=90°,
∴AO=AB•cos∠BAO=$\sqrt{3}$,BO=AB•sin∠BAO=1.
同理可知:A′O=$\sqrt{3}$,D′O=1,
∴AD′=AO-D′O=$\sqrt{3}$-1.
∵∠A′D′O=90°-30°=60°,∠BAO=30°,
∴∠AED′=30°=∠EAD′,
∴D′E=AD′=$\sqrt{3}$-1.
在Rt△ED′F中,ED′=$\sqrt{3}$-1,∠ED′F=60°,
∴EF=ED′•sin∠ED′F=$\frac{3-\sqrt{3}}{2}$.
∴S阴影=S菱形ABCD+4S△AD′E=$\frac{1}{2}$×2AO×2BO+4×$\frac{1}{2}$AD′•EF=6$\sqrt{3}$-6.
故答案为:6$\sqrt{3}$-6.
点评 本题考查了菱形的性质、旋转的性质、解直角三角形、菱形的面积公式以及三角形的面积公式,解题的关键是求出△AD′E的面积.本题属于中档题,难度不小,历年来时常会考到周长,今年碰到了求面积,解决该题的技巧是分割图形,将阴影部分分割成菱形与四个全等的三角形,求出其中任意一个三角形的面积是解决本题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.
光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
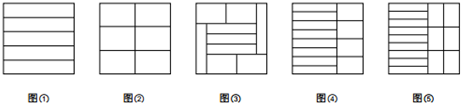
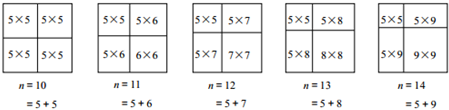
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.
我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com