
 如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为2.
如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为2. 分析 根据三角形中位线定理依次可求得第二个三角形和第三个三角形的周长,可找出规律,进而可求得第6个三角形的周长.
解答 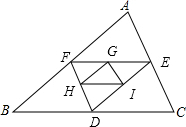 解:
解:
如图,∵E、F分别为AB、AC的中点,
∴EF=$\frac{1}{2}$BC,同理可得DF=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AB,
∴EF+DF+DE=$\frac{1}{2}$(AB+BC+CA),
即△DEF的周长=$\frac{1}{2}$△ABC的周长,
∴第二个三角形的周长是原三角形周长的$\frac{1}{2}$,
同理可得△GHI的周长=$\frac{1}{2}$△DEF的周长=$\frac{1}{4}$△ABC的周长=($\frac{1}{2}$)2△ABC的周长,
∴第三个三角形的周长是原三角形周长的($\frac{1}{2}$)2,
∴第六个三角形的周长是原三角形周长的($\frac{1}{2}$)5=$\frac{1}{32}$,
∵原三角形的三边长为30,48,50,
∴原三角形的周长为128,
∴第一个新三角形的周长为64,
∴第六个三角形的周长=64×$\frac{1}{32}$=2
故答案为:2.
点评 本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,AB=3,BC=5,CA=6,AC的垂直平分线分别交AC、BC于点D、E,则△ABE的周长为( )
如图所示,在△ABC中,AB=3,BC=5,CA=6,AC的垂直平分线分别交AC、BC于点D、E,则△ABE的周长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4,∠AOD=60°,则AB的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4,∠AOD=60°,则AB的长为( )| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )| A. | 4 | B. | 8 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
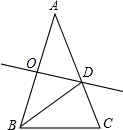 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,为测池塘AB的宽度,在池塘外选一点P,分别取线段PA、PB的中点C、D,测得CD的长就能知道AB的长.其中的数学根据是三角形的中位线等于第三边的一半.
如图,为测池塘AB的宽度,在池塘外选一点P,分别取线段PA、PB的中点C、D,测得CD的长就能知道AB的长.其中的数学根据是三角形的中位线等于第三边的一半.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-2$\sqrt{3}$=1 | B. | $\root{3}{-27}$=-3 | C. | |$\sqrt{2}$-$\sqrt{3}$|+$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{3}$ | D. | ($\sqrt{3}$+$\frac{1}{\sqrt{3}}$)÷$\sqrt{3}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=4cm,∠ABC=60°,则四边形EFGH的面积为4$\sqrt{3}$cm2.
如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=4cm,∠ABC=60°,则四边形EFGH的面积为4$\sqrt{3}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com