
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
【答案】(1)W=![]() ;(2)李师傅第8天创造的利润最大,最大利润是324元;(3)李师傅共可获得160元奖金.
;(2)李师傅第8天创造的利润最大,最大利润是324元;(3)李师傅共可获得160元奖金.
【解析】(1)根据题意和表格中的数据可以求得p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)根据题意和题目中的函数表达式可以解答本题;
(3)根据(2)中的结果和不等式的性质可以解答本题.
(1)设p与x之间的函数关系式为p=kx+b,则有
![]() ,解得,
,解得,![]() ,
,
即p与x的函数关系式为p=0.5x+7(1≤x≤15,x为整数),
当1≤x<10时,
W=[20﹣(0.5x+7)](2x+20)=﹣x2+16x+260,
当10≤x≤15时,
W=[20﹣(0.5x+7)]×40=﹣20x+520,
即W=![]() ;
;
(2)当1≤x<10时,
W=﹣x2+16x+260=﹣(x﹣8)2+324,
∴当x=8时,W取得最大值,此时W=324,
当10≤x≤15时,
W=﹣20x+520,
∴当x=10时,W取得最大值,此时W=320,
∵324>320,
∴李师傅第8天创造的利润最大,最大利润是324元;
(3)当1≤x<10时,
令﹣x2+16x+260=299,得x1=3,x2=13,
当W>299时,3<x<13,
∵1≤x<10,
∴3<x<10,
当10≤x≤15时,
令W=﹣20x+520>299,得x<11.05,
∴10≤x≤11,
由上可得,李师傅获得奖金的月份是4月到11月,李师傅共获得奖金为:20×(11﹣3)=160(元),
即李师傅共可获得160元奖金.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
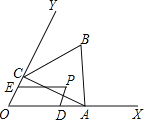
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.
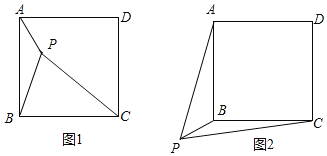
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司分两次采购甲、乙两种商品,具体情况如下:
商品 | 甲 | 乙 | 花费资金 |
次数 | |||
第一次采购件数 | 10件 | 15件 | 350元 |
第二次采购件数 | 15件 | 10件 | 375元 |
(1)求甲、乙商品每件各多少元?
(2)公司计划第三次采购甲、乙两种商品共31件,要求花费资金不超过475元,问最多可购买甲商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
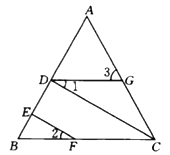
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=8,则线段BD+CE的长为
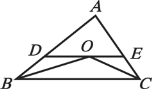
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
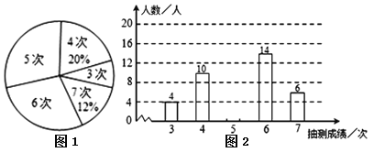
【题目】为了解某校八年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)本次抽测的男生有 人,抽测成绩的众数是 ;
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校400名八年级男生中估计有多少人体能达标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com