
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
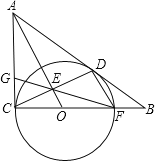
【答案】
【解析】
试题分析:(1)欲证明DF∥OA,只要证明OA⊥CD,DF⊥CD即可;
(2)过点作EM⊥OC于M,易知![]() ,只要求出EM、FM、FC即可解决问题;
,只要求出EM、FM、FC即可解决问题;
试题解析:(1)证明:连接OD.
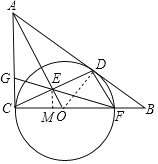
∵AB与⊙O相切与点D,又AC与⊙O相切与点,
∴AC=AD,∵OC=OD,
∴OA⊥CD,
∴CD⊥OA,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC=![]() =8,
=8,
∴AD=AC=6,
∴BD=AB-AD=4,
∵BD2=BFBC,
∴BF=2,
∴CF=BC-BF=6.OC=![]() CF=3,
CF=3,
∴OA=![]() =3
=3![]() ,
,
∵OC2=OEOA,
∴OE=![]() ,
,
∵EM∥AC,
∴![]() ,
,
∴OM=![]() ,EM=
,EM=![]() ,FM=OF+OM=
,FM=OF+OM=![]() ,
,
∴![]() ,
,
∴CG=![]() EM=2.
EM=2.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a-b|=2016,且AO=2BO,则a+b的值为______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
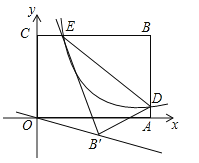
【题目】如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数![]() 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
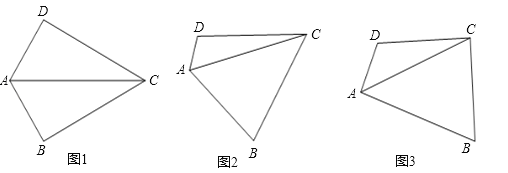
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
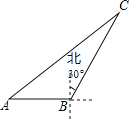
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC且BD>CD,DF⊥AB,△CDE和△ADB都是等腰直角三角形,给出下列结论,正确的是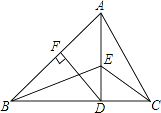
①△ADC≌△BDE;
②△ADF≌△BDF;
③△CDE≌△AFD;
④△ACE≌ABE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com