
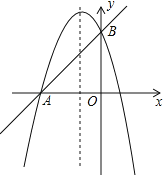
【题目】如图,已知抛物线![]() 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)C(﹣1,4);(3)(﹣1,4)或(﹣2,3)或(
;(2)C(﹣1,4);(3)(﹣1,4)或(﹣2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)把点A,B两点的坐标分别代入抛物线解析式,求出b和c的值即可;
(2)过点B作CB⊥AB,交抛物线的对称轴于点C,过点C作CE⊥y轴,垂足为点E,求出点C的横坐标,再求出OE的长,即可得到点C的纵坐标;
(3)假设在在抛物线上存在点P,使得△APB的面积等于3,连接PA,PB,过P作PD⊥AB于点D,作PF∥y轴交AB于点F,在Rt△OAB中,易求AB=![]() ,设点P的坐标为(m,
,设点P的坐标为(m,![]() ),设点F的坐标为(m,m+3),再分两种情况讨论:①当点P在直线AB上方时,②当点P在直线AB下方时,分别求出符合条件点P的坐标即可.
),设点F的坐标为(m,m+3),再分两种情况讨论:①当点P在直线AB上方时,②当点P在直线AB下方时,分别求出符合条件点P的坐标即可.
试题解析:(1)把点A(﹣3,0),B(0,3)代入![]() 得:
得:![]() ,解得:
,解得:![]() ,∴抛物线的解析式是
,∴抛物线的解析式是![]() ;
;
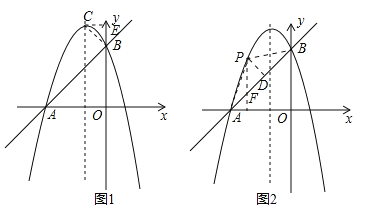
(2)如图1:过点B作CB⊥AB,交抛物线的对称轴于点C,过点C作CE⊥y轴,垂足为点E,∵![]() ,∴抛物线对称轴为直线x=﹣1,∴CE=1,∵AO=BO=1,∴∠ABO=45°,∴∠CBE=45°,∴BE=CE=1,∴OE=OB+BE=4,∴点C的坐标为(﹣1,4);
,∴抛物线对称轴为直线x=﹣1,∴CE=1,∵AO=BO=1,∴∠ABO=45°,∴∠CBE=45°,∴BE=CE=1,∴OE=OB+BE=4,∴点C的坐标为(﹣1,4);
(3)假设在在抛物线上存在点P,使得△APB的面积等于3,如图2:连接PA,PB,过P作PD⊥AB于点D,作PF∥y轴交AB于点F,在Rt△OAB中,易求AB=![]() =
=![]() ,∵S△APB=3,∴PD=
,∵S△APB=3,∴PD=![]() ,∵∠PFD=∠ABO=45°,∴PF=
,∵∠PFD=∠ABO=45°,∴PF=![]() ,设点P的坐标为(m,
,设点P的坐标为(m,![]() ),∵A(﹣3,0),B(0,3),∴直线AB的解析式为
),∵A(﹣3,0),B(0,3),∴直线AB的解析式为![]() ,∴可设点F的坐标为(m,m+3),
,∴可设点F的坐标为(m,m+3),
①当点P在直线AB上方时,可得:![]() ,解得:m=﹣1或﹣2,∴符合条件的点P坐标为(﹣1,4)或(﹣2,3),
,解得:m=﹣1或﹣2,∴符合条件的点P坐标为(﹣1,4)或(﹣2,3),
②当点P在直线AB下方时,可得:![]() ,解得:m=
,解得:m=![]() 或
或![]() ,∴符合条件的点P坐标为(
,∴符合条件的点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上可知符合条件的点P有4个,坐标分别为:(﹣1,4)或(﹣2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】下列各题正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由 ![]() =1+
=1+ ![]() 去分母得2(2x﹣1)=1+3(x﹣3)
去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7去括号、移项、合并同类项得x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)2(m+1)2﹣(2m+1)(2m﹣1);
(2)4x2﹣(﹣2x+3)(﹣2x﹣3);
(3)先化简,再求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式;
(2)若α为锐角,tanα=![]() ,当AE取得最小值时,求正方形OEFG的面积;
,当AE取得最小值时,求正方形OEFG的面积;
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为![]() :1?若能,求点P的坐标;若不能,试说明理由.
:1?若能,求点P的坐标;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲是乙现在的年龄时,乙8岁,乙是甲现在的年龄时,甲26岁,那么( )
A. 甲比乙大6岁 B. 甲比乙大9岁
C. 乙比甲大18岁 D. 乙比甲大34岁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式: ①(2a+b)(m+n); ②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b); ④2am+2an+bm+bn,你认为其中正确的有( )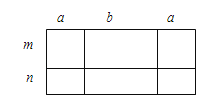
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各多项式中,能用公式法分解因式的是( )
A. a2-b2+2ab B. a2+b2+ab C. 25n2+15n+9 D. 4a2+12a+9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com