
【题目】规律发现:
在数轴上
(1)点M表示的数是2,点N表示的数是8,则线段MN的中点P表示的数为______;
(2)点M表示的数是﹣3,点N表示的数是7,则线段MN的中点P表示的数为_____;发现:点M表示的数是a,点N表示的数是b,则线段MN的中点P表示的数为______.
直接运用:
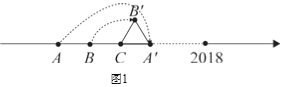
将数轴按如图1所示,从点A开始折出一个等边三角形A'B'C,设点A表示的数为x﹣3,点B表示的数为2x+1,C表示的数为x﹣1,则x值为_____,若将△A'B'C从图中位置向右滚动,则数2018对应的点将与△A'B'C的顶点_______重合.
类比迁移:
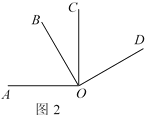
如图2:OA⊥OC,OB⊥OD,∠COD=60°,若射线OA绕O点以每秒15°的速度顺时针旋转,射线OB绕O点以每秒10°的速度顺时针旋转,射线OC绕O点以每秒5°的速度逆时针旋转,三线同时旋转,当一条射线与射线OD重合时,三条射线同时停止运动.
①求射线OC和射线OB相遇时,∠AOB的度数;
②运动几秒时,射线OA是∠BOC的平分线?
【答案】规律发现:(1)5;(2)2,![]() ;直接运用:-3,C;类比迁移:①∠AOB=50°;②运动6秒时,OA是∠BOC的平分线.
;直接运用:-3,C;类比迁移:①∠AOB=50°;②运动6秒时,OA是∠BOC的平分线.
【解析】
(1)规律发现:根据线段的中点的定义解答即可;
(2)直接运用:根据等边三角形ABC边长相等,求出x的值,再利用数字2018对应的点与![]() 的距离,求得C从出发到2018点滚动的周数,即可得出答案;
的距离,求得C从出发到2018点滚动的周数,即可得出答案;
类比迁移:①设x秒后射线OC和射线OB相遇,可得方程![]() ,解方程求出t的值,即可求出
,解方程求出t的值,即可求出![]() 的度数;
的度数;
②设y秒时,射线OA是![]() 的平分线,可得方程
的平分线,可得方程![]() ,解方程即可解答.
,解方程即可解答.
解:(1)点M表示的数是2,点N表示的数是8,则线段MN的中点P表示的数为![]() ,
,
故答案为:5;
(2)点M表示的数是3,点N表示的数是7,则线段MN的中点P表示的数为![]() ,
,
故答案为:2;
发现:点M表示的数是a,点N表示的数是b,则线段MN的中点P表示的数为![]() ;
;
故答案为:![]() ;
;
直接运用:
∵将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x3,点B表示的数为2x+1,点C表示的数为4,
∴4(2x+1)=2x+1(x3);
∴3x=9,
x=3.
故A表示的数为:x3=33=6,
点B表示的数为:2x+1=2×(3)+1=5,
即等边三角形ABC边长为1,
数字2018对应的点与4的距离为:2018+4=2022,
∵2022÷3=674,C从出发到2018点滚动674周,
∴数字2018对应的点将与△ABC的顶点C重合;
类比迁移:
① ∵OB⊥OD
∴∠DOB=90°
∵∠COD=60°
∴∠BOC=∠DOB- ∠COD =30°
设运动t秒时射线OB和射线OC相遇
根据题意得:5t+10t=30
解之得:t=2
此时∠AOB=60°+10°×2-15°×2=50°;
②设运动x秒时OA是∠BOC的平分线
15x+5x﹣90=60+10x﹣15x
解得x=6.
故运动6秒时,OA是∠BOC的平分线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=kx+b的图象与y轴交于点B(0,1),与反比例函数y=![]() 的图象交于点A(3,﹣2).
的图象交于点A(3,﹣2).
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且BC=BA,直接写出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
(1)若∠FAE=20°,求∠DCG的度数;
(2)猜想:AF,FG,CG三者之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() 、射线
、射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() ;
;![]() 、
、![]() 同时出发,同时射线
同时出发,同时射线![]() 绕着点
绕着点![]() 从
从![]() 上以每秒5°的速度顺时针旋转,设运动时间是
上以每秒5°的速度顺时针旋转,设运动时间是![]() .
.
(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 为何值时,
为何值时,![]() ?此时射线
?此时射线![]() 是
是![]() 的角平分线吗?如果是请说明理由.
的角平分线吗?如果是请说明理由.
(3)在射线![]() 上是否存在
上是否存在![]() 、
、![]() 相距
相距![]() ?若存在,请求出t的值并求出此时
?若存在,请求出t的值并求出此时![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域交流越来越深,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动.据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的![]() 还少25万件,求北京故宫博物院约有多少万件藏品?
还少25万件,求北京故宫博物院约有多少万件藏品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,点
上的一个动点,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(1)若点![]() 恰好是
恰好是![]() 中点,则
中点,则![]()
![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)试利用“字母代替数”的方法,说明不论![]() 取何值(不超过
取何值(不超过![]() ),
),![]() 的长不变.
的长不变.

查看答案和解析>>
科目:初中数学 来源: 题型:
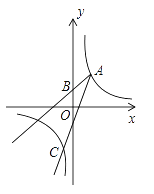
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com