
| A. | 5 | B. | 5或$\sqrt{6}$ | C. | $\sqrt{5}$ | D. | 5或$\sqrt{7}$ |
分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4,既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为x
(1)若4是直角边,则第三边x是斜边,由勾股定理,得
32+42=x2,所以x=5
(2)若4是斜边,则第三边x为直角边,由勾股定理,得
32+x2=42,所以x=$\sqrt{7}$.
所以第三边的长为5或$\sqrt{7}$.
故选D.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
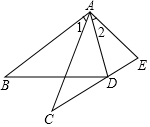 如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )| A. | BD=CE | B. | AD=AE | C. | ∠B=∠C | D. | ∠ADB=∠AEC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 8 | 10 | 9 | 6 | 9 |
| 乙 | 10 | 8 | 9 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
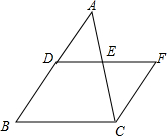 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(4,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-1,0)或(1,8).
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(4,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-1,0)或(1,8).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
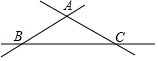 如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )
如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )| A. | 6、12、6 | B. | 6、10、6 | C. | 4、12、4 | D. | 4、8、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com