
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数![]() 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.
下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=45°,MN=2,则点C的坐标为![]() .
.
其中正确的个数是( )
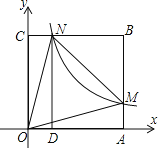
A.1B.2C.3D.4
【答案】C
【解析】
根据反比例函数的比例系数的几何意义得到S△ONC=S△OAM=![]() k,即
k,即![]() OCNC=
OCNC=![]() OAAM,而OC=OA,则NC=AM,在根据“SAS”可判断△OCN≌△OAM;根据全等的性质得到ON=OM,由于k的值不能确定,则∠MON的值不能确定,无法确定△ONM为等边三角形,则ON不一定等于MN;根据S△OND=S△OAM=
OAAM,而OC=OA,则NC=AM,在根据“SAS”可判断△OCN≌△OAM;根据全等的性质得到ON=OM,由于k的值不能确定,则∠MON的值不能确定,无法确定△ONM为等边三角形,则ON不一定等于MN;根据S△OND=S△OAM=![]() k和S△OND+S四边形DAMN=S△OAM+S△OMN,即可得到S四边形DAMN=S△OMN;作NE⊥OM于E点,则△ONE为等腰直角三角形,设NE=x,则OM=ON=
k和S△OND+S四边形DAMN=S△OAM+S△OMN,即可得到S四边形DAMN=S△OMN;作NE⊥OM于E点,则△ONE为等腰直角三角形,设NE=x,则OM=ON=![]() x,EM=
x,EM=![]() x-x=(
x-x=(![]() -1)x,在Rt△NEM中,利用勾股定理可求出x2=2+
-1)x,在Rt△NEM中,利用勾股定理可求出x2=2+![]() ,所以ON2=(
,所以ON2=(![]() x)2=4+2
x)2=4+2![]() ,易得△BMN为等腰直角三角形,得到BN=
,易得△BMN为等腰直角三角形,得到BN=![]() MN=
MN=![]() ,设正方形ABCO的边长为a,在Rt△OCN中,利用勾股定理可求出a的值为
,设正方形ABCO的边长为a,在Rt△OCN中,利用勾股定理可求出a的值为![]() +1,从而得到C点坐标为(0,
+1,从而得到C点坐标为(0,![]() +1).
+1).
∵点M、N都在y=![]() 的图象上,
的图象上,
∴S△ONC=S△OAM=![]() k,即
k,即![]() OCNC=
OCNC=![]() OAAM,
OAAM,
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴NC=AM,
∴△OCN≌△OAM,所以①正确;
∴ON=OM,
∵k的值不能确定,
∴∠MON的值不能确定,
∴△ONM只能为等腰三角形,不能确定为等边三角形,
∴ON不一定等于MN,所以②错误;
∵S△OND=S△OAM=![]() k,
k,
而S△OND+S四边形DAMN=S△OAM+S△OMN,
∴四边形DAMN与△MON面积相等,所以③正确;
作NE⊥OM于E点,如图,
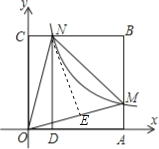
∵∠MON=45°,
∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则ON=![]() x,
x,
∴OM=![]() x,
x,
∴EM=![]() x-x=(
x-x=(![]() -1)x,
-1)x,
在Rt△NEM中,MN=2,
∵MN2=NE2+EM2,即22=x2+[(![]() -1)x]2,
-1)x]2,
∴x2=2+![]() ,
,
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴BN=![]() MN=
MN=![]() ,
,
设正方形ABCO的边长为a,则OC=a,CN=a-![]() ,
,
在Rt△OCN中,∵OC2+CN2=ON2,
∴a2+(a-![]() )2=4+2
)2=4+2![]() ,解得a1=
,解得a1=![]() +1,a2=-1(舍去),
+1,a2=-1(舍去),
∴OC=![]() +1,
+1,
∴C点坐标为(0,![]() +1),所以④正确.
+1),所以④正确.
故选:C.


科目:初中数学 来源: 题型:
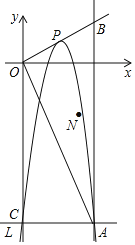
【题目】如图,点P为抛物线L:y=a(x﹣2)(x﹣4)(其中a为常数,且a<0)的顶点,L与y轴交于点C,过点C作x轴的平行线,与L交于点A,过点A作x轴的垂线,与射线OP交于点B,连接OA
(1)a=﹣2时,点P的坐标是 ,点B的坐标是 ;
(2)是否存在a的值,使OA=OB?若存在,求出a的值;若不存在,请说明理由
(3)若△OAB的外心N的坐标为(p,q),则
①当点N在△OAB内部时,求a的取值范围;
②用a表示外心N的横坐标p和纵坐标q,并求p与q的关系式(不写q的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
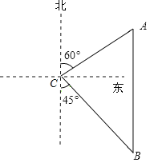
【题目】如图,一艘轮船从位于灯塔![]() 的北偏东60°方向,距离灯塔60海里的小岛
的北偏东60°方向,距离灯塔60海里的小岛![]() 出发,沿正南方向航行一段时间后,到达位于灯塔
出发,沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东45°方向上的
的南偏东45°方向上的![]() 处,这时轮船
处,这时轮船![]() 与小岛
与小岛![]() 的距离是__________海里.
的距离是__________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的部分对应值如表:
![]()
利用该二次函数的图象判断,当函数值y>0时,x的取值范围是( )
A.0<x<8B.x<0或x>8C.﹣2<x<4D.x<﹣2或x>4
查看答案和解析>>
科目:初中数学 来源: 题型:
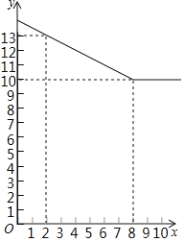
【题目】果农周大爷家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,他记录了10天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如表所示:

(1)请直接写出p与x的函数关系式及自变量x的取值范围;
(2)求y与x的函数关系式,并写出自变量x的取值范围;
(3)在这10天中,哪一天销售额达到最大,最大销售额是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
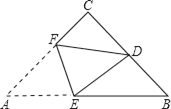
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
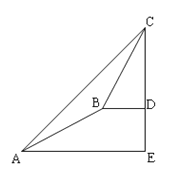
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为45°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走4米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.

(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的动点,且满足
是抛物线上的动点,且满足![]() ,求出
,求出![]() 点的坐标;
点的坐标;
(3)连接![]() ,点
,点![]() 是
是![]() 轴一动点,点
轴一动点,点![]() 是抛物线上一动点,若以
是抛物线上一动点,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
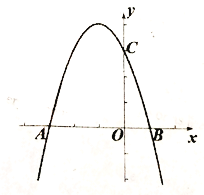 备用图
备用图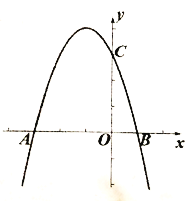
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com