
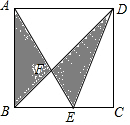
 如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )| A. | $\frac{1}{3}$SABCD | B. | $\frac{1}{6}$SABCD | C. | $\frac{1}{2}$SABCD | D. | $\frac{1}{9}$SABCD |
分析 设正方形的边长为a,AE与BD相交于F点,如图,由AD∥BC可判断△ADF∽△EBF,于是利用三角形面积公式可得S△ABF=S△DEF=2S△BEF,而S△ABE=$\frac{1}{4}$a2所以S△DCF=S△EBF=$\frac{2}{3}$×$\frac{1}{4}$a2=$\frac{1}{6}$a2,然后计算图中阴影部分的面积.
解答 解:AE与BD相交于F点,如图,
∵E为BC的中点,
∴BE=$\frac{1}{2}$ AD
AD
∵AD∥BE,
∴△ADF∽△EBF,
∴$\frac{AF}{EF}$=$\frac{AD}{BE}$=2,
∴S△ABF=S△DEF=2S△BEF,
而S△ABE=$\frac{1}{2}$×$\frac{1}{2}$a×a=$\frac{1}{4}$a2,
∴S△ABF=S△DEF=$\frac{2}{3}$×$\frac{1}{4}$a2=$\frac{1}{6}$a2,
∴图中阴影部分的面积=2×S△ABF=$\frac{1}{3}$a2=$\frac{1}{3}$SABCD.
故选A.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质和三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{y-2}{3}$ | B. | x=$\frac{2-y}{3}$ | C. | y=3x-2 | D. | y=2-3x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.
如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
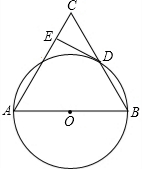 如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.
如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com