
【题目】1号探测气球从海拔5 m处出发,以l m/min的速度上升.与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升,两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50).
(1)根据题意,填写下表:
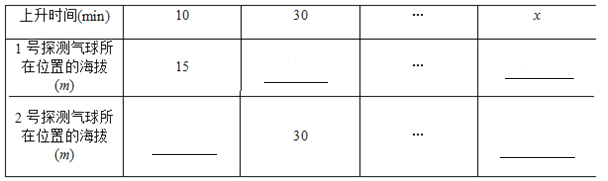
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
【答案】(1)20,35,x+5,0.5x+15;(2)此时气球上升了20 min,都位于海拔25 m的高度.(3)15 m.
【解析】试题分析:(Ⅰ)由题意可得,1号探测气球从海拔5 m处出发,以1m/min的速度上升,30min时1号探测气球的海拔高度为35m,xmin时海拔高度为(x+5)m;2号探测气球从海拔15m处出发,以0.5m/min的速度上升,10min时2号探测气球的海拔高度为20m,xmin时海拔高度为(0.5x+15)m.
(Ⅱ)令x+5=0.5x+15,若x有解且x的值位于0≤x≤50这个范围,则说明在某时刻两个气球能位于同一高度,这时求得x的值再带入求气球的海拔高度即可,若x有解且x的值不位于0≤x≤50这个范围,则不存在某时刻两个气球位于同一高度.
(Ⅲ)当30≤x≤50时,由题意,可知1号气球所在位置的海拔始终高于2号气球,设两个气球在同一时刻所在位置的海拔相差有y米,用x表示出y,根据所得的关系式及x的取值范围,即可求得两个气球所在位置的海拔高度相差的最大值.
试题解析:(Ⅰ)35,x+5;20,0.5x+15.
(Ⅱ)两个气球能位于同一高度.
根据题意,x+5=0.5x+15,解得x=20.
有x+5=25.
答:此时,气球上升了20min,都位于海拔25m的高度.
(Ⅲ))当30≤x≤50时,
由题意,可知1号气球所在位置的海拔始终高于2号气球,
设两个气球在同一时刻所在位置的海拔相差有y米,
则y=(x+5)—(0.5x+15)=0.5x—10.
∵0.5>0,
∴y随x的增大而增大.
∴当x=50时,y取得最大值15.
答:两个气球所在位置的海拔最多相差15米.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】下列语句正确的个数为 ( )
①圆是立体图形:②射线只有一个端点;③线段AB就是A、B两点之间的距离:④等角的余角相等
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
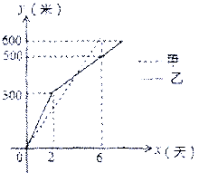
【题目】据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题。现有甲、乙两工程队分别同时修建两条600米长的道路,己知修建道路长度![]() (米)与修建时间
(米)与修建时间![]() (天)之间的关系如图所示,则下列说法中错误的是( )
(天)之间的关系如图所示,则下列说法中错误的是( )
A.甲队每天修建100米;
B. 第6天,甲队比乙队多修建100米;
C.乙队开工两天后,每天修建50米;
D. 甲队比乙队提前3天完成任务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法,按括号内的要求对下列各数求近似值:
3.5952(精确到0.01);
60340(保留两个有效数字);
23.45(精确到个位);
4.736×105(精确到千位) ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com