
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
科目:初中数学 来源: 题型:
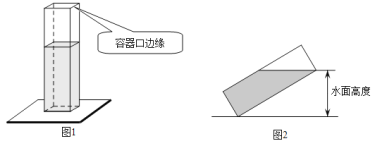
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多
型空气净化器的进价多![]() 元,用
元,用![]() 元购进
元购进![]() 型空气净化器和用
型空气净化器和用![]() 元购进
元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)商社电器计划![]() 型净化器的进货量不少于
型净化器的进货量不少于![]() 台且是
台且是![]() 型净化器进货量的三倍,在总进货款不超过
型净化器进货量的三倍,在总进货款不超过![]() 万元的前提下,试问有多少种进货方案?
万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
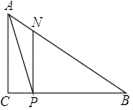
【题目】如图在△ABC中,∠C=90°,AC=3cm,BC=4cm,点P是边BC上由B向C运动(不与点B、C重合)的一动点,P点的速度是1cm/s,设点P的运动时间为t,过P点作AC的平行线交AB与点N,连接AP,
(1)请用含有t的代数式表示线段AN和线段PN的长,
(2)当t为何值时,△APN的面积等于△ACP面积的三分之一?
(3)在点P的运动过程中,是否存在某一时刻的t的值,使得△APN的面积有最大值,若存在请求出t的值并计算最大面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
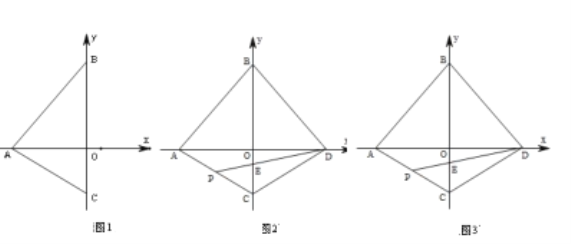
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() .
.
(1)求![]() 的值;
的值;
(2)把![]() 沿
沿![]() 轴翻折,使点
轴翻折,使点![]() 落在
落在![]() 轴的点
轴的点![]() 处,点
处,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 横坐标为
横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 、
、![]() 的函数解析式(用含
的函数解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)在(2)的条件下,若![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=![]() x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间B.256元/间C.258元/间D.260元/间
查看答案和解析>>
科目:初中数学 来源: 题型:
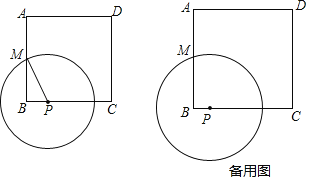
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.
(1)当BP= 时,△MBP~△DCP;
(2)当⊙P与正方形ABCD的边相切时,求BP的长;
(3)设⊙P的半径为x,请直接写出正方形ABCD中恰好有两个顶点在圆内的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点![]() 的两条直线分别交
的两条直线分别交![]() 轴于
轴于![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 两点的纵坐标分别是一元二次方程
两点的纵坐标分别是一元二次方程![]() 的两个根.
的两个根.
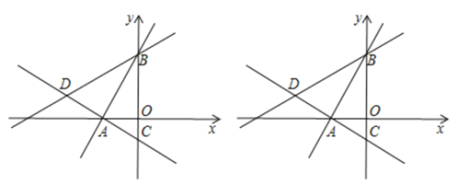
(1)试问:直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在直线![]() 上寻找点
上寻找点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,请直接写出
三点为顶点的三角形是等腰三角形,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
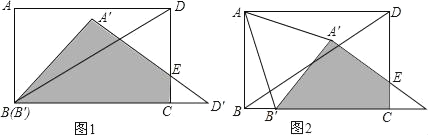
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 绕
绕![]() 点作顺时针方向旋转得到
点作顺时针方向旋转得到![]() (
(![]() 与
与![]() 重合),且点
重合),且点![]() 刚好落在
刚好落在![]() 的延长上,
的延长上,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求矩形![]() 与
与![]() 重叠部分(如图1中阴影部分
重叠部分(如图1中阴影部分![]() )的面积;
)的面积;
(2)将![]() 以每秒2
以每秒2![]() 的速度沿直线
的速度沿直线![]() 向右平移,如图2,当
向右平移,如图2,当![]() 移动到
移动到![]() 点时停止移动.设矩形
点时停止移动.设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,移动的时间为
,移动的时间为![]() ,请你直接写出
,请你直接写出![]() 关于
关于![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的平移过程中,是否存在这样的时间![]() ,使得
,使得![]() 成为等腰三角形?若存在,请你直接写出对应的
成为等腰三角形?若存在,请你直接写出对应的![]() 的值,若不存在,请你说明理由.
的值,若不存在,请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com