练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若a2-b2=8，a-b=2，则a+b的值为4．

    分析 a2-b2=8，即（a+b）（a-b）=8，把a-b=2代入即可求得．

    解答 解：a2-b2=8，即（a+b）（a-b）=8，
    ∵a-b=2，
    ∴a+b=4．
    故答案为：4．

    点评 本题考查了平方差公式，运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，一边长为30cm，宽20cm的长方形铁皮，四角各截去一个大小相同的正方形，将四边折起，可以做成一个无盖长方体容器，求所得容器的容积V关于截去的小正方形的边长x的函数关系式，并指出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图是利用平面直角坐标系画出的怀柔城区附近部分乡镇分布图．若这个坐标系分别以正东、正北方向为x轴、y轴的正方向．表示南华园村的点坐标为（0，-1），表示下园村的点的坐标为（1.6，0.9），则表示下列各地的点的坐标正确的是（　　）
    A．石厂村（-1.2，-2.7）B．怀柔镇（0.4，1）C．普法公园（0，0）D．大屯村（2.2，2.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．记20162的所有正约数为d1，d2，…，dm，则$\frac{1}{{d}_{1}+2016}$+$\frac{1}{{d}_{2}+2016}$+…+$\frac{1}{{d}_{m}+2016}$=$\frac{165}{4032}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知抛物线 y=x2-2x-3
    （1）此抛物线的顶点坐标是（1，-4），与x轴的交点坐标是（3，0），（-1，0），与y轴交点坐标是（0，-3），对称轴是x=1
    （2）在平面直角坐标系中画出y=x2-2x-3的图象；
    （3）结合图象，当x取何值时，y随x的增大而减小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

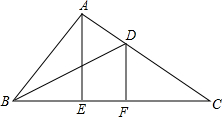    3．在△ABC中，AE⊥BC于点E，∠BAE：∠CAE=4：7，BD平分∠ABC，点F在BC上，∠CDF=70°，∠ABD=25°．
    （1）求∠CAE的度数；
    （2）求证：DF⊥BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．第48届世界乒乓球锦标赛于2005年4月30日至5月6日在上海举行，中国选手包揽了全部五个单项的冠军．已知5月3日一天的单打（一对一）比赛和双打（二对二）比赛共进行了68场，参赛运动员共有208人次．问5月3日这一天举行了几场单打比赛、几场双打比赛？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知：如图，在平面直角坐标系中．
    （1）作出△ABC 关于y轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标：A1（0，-2），B1（-2，-4），C1（-4，-1）；
    （2）直接写出△ABC的面积为5；
    （3）在x轴上画点P，使PA+PC最小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在8×8的方格纸中建立平面直角坐标系，已知A（2，4）、B（4，2）．C是第一象限内的一个格点，且点C与线段AB可以组成一个以AB为底、腰长为无理数的等腰三角形．
    （1）点C的坐标是（1，1），△ABC的面积是4；
    （2）将△ABC绕点C旋转180°，得△A1B1C1，连接AB1、BA1，试判断四边形AB1A1B是何种特殊的四边形？并说明理由．

    查看答案和解析>>

    同步练习册答案