

分析 (1)在AE上取一点F,使AF=AB,及可以得出△ACB≌△ACF,就可以得出BC=FC,∠ACB=∠ACF,就可以得出△CEF≌△CED.就可以得出结论;
(2)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等边三角形,就有FG=CG=$\frac{1}{2}$BD,进而得出结论;
(3)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等腰直角三角形,由勾股定理求出FG的值就可以得出结论.
解答 解:(1)AE=AB+DE;
理由:在AE上取一点F,使AF=AB.如图1
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠BAC=∠FAC}\\{AC=AC}\end{array}\right.$,
∴△ACB≌△ACF(SAS),
∴BC=FC,∠ACB=∠ACF.
∵C是BD边的中点.
∴BC=CD,
∴CF=CD.
∵∠ACE=90°,
∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°
∴∠ECF=∠ECD.
在△CEF和△CED中,
$\left\{\begin{array}{l}{CF=CD}\\{∠ECF=∠ECD}\\{CE=CE}\end{array}\right.$,
∴△CEF≌△CED(SAS),
∴EF=ED.
∵AE=AF+EF,
∴AE=AB+DE,
故答案为:AE=AB+DE;
(2)猜想:AE=AB+DE+$\frac{1}{2}$BD.
证明:如图(2),在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.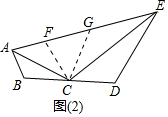
∵C是BD边的中点,
∴CB=CD=$\frac{1}{2}$BD.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠BAC=∠FAC}\\{AC=AC}\end{array}\right.$,
∴△ACB≌△ACF(SAS),
∴CF=CB,
∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.
∵CB=CD,∴CG=CF
∵∠ACE=120°,
∴∠BCA+∠DCE=180°-120°=60°.
∴∠FCA+∠GCE=60°.
∴∠FCG=60°.
∴△FGC是等边三角形.
∴FG=FC=$\frac{1}{2}$BD.
∵AE=AF+EG+FG.
∴AE=AB+DE+$\frac{1}{2}$BD.
(3)如图(3),在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.
∵C是BD边的中点,
∴CB=CD=$\frac{1}{2}$BD.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠BAC=∠FAC}\\{AC=AC}\end{array}\right.$,
∴△ACB≌△ACF(SAS),
∴CF=CB,∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.
∵CB=CD,∴CG=CF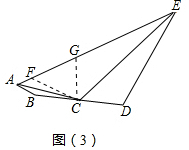
∵∠ACE=135°,
∴∠BCA+∠DCE=180°-135°=45°.
∴∠FCA+∠GCE=45°.
∴∠FCG=90°.
∴△FGC是等腰直角三角形.
∴FC=$\frac{1}{2}$BD.
∵BD=8,
∴FC=4,
∴FG=4$\sqrt{3}\sqrt{3}$.
∵AE=AF+FG+GE,
∴AE=AB+4$\sqrt{2}$+DE.
∵AB=2,DE=8,
∴AE=AF+FG+EG=10+4$\sqrt{2}$.
点评 本题考查了和四边形有关的综合性题目,用到的知识点有:角平分线的性质的运用,全等三角形的判定及性质的运用,等边三角形的性质的运用,勾股定理的运用,解答时证明三角形全等是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.
已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
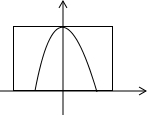 如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )
如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )| A. | 2.52米 | B. | 2.88米 | C. | 2.97米 | D. | 3.12米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com