
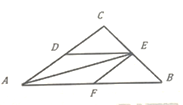
【题目】如图,在△ABC中,AB=3+![]() ,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
【答案】![]()
【解析】
如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.由四边形ADEF是菱形,推出F,D关于直线AE对称,推出PF=PD,推出PF+PB=PA+PB,由PD+PB≥BD,推出PF+PB的最小值是线段BD的长.
如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.
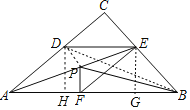
∵四边形ADEF是菱形,
∴F,D关于直线AE对称,
∴PF=PD,
∴PF+PB=PA+PB,
∵PD+PB≥BD,
∴PF+PB的最小值是线段BD的长,
∵∠CAB=180°-105°-45°=30°,设AF=EF=AD=x,则DH=EG=![]() x,FG=
x,FG=![]() x,
x,
∵∠EGB=45°,EG⊥BG,
∴EG=BG=![]() x,
x,
∴x+![]() x+
x+![]() x=3+
x=3+![]() ,
,
∴x=2,
∴DH=1,BH=3,
∴BD=![]() =
=![]() ,
,
∴PF+PB的最小值为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
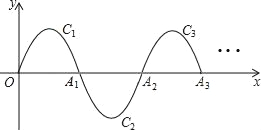
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.若P(50,m)在第17段抛物线C17上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是平面上的一点,且
是平面上的一点,且![]() ,连接
,连接![]() .
.
(1)如图,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
(2)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(3)将点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
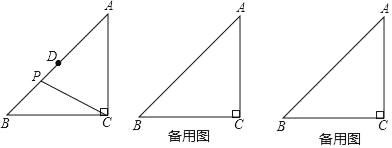
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,D是线段AC延长线上一点,连接BD,过点A作
,D是线段AC延长线上一点,连接BD,过点A作![]() 于E.
于E.
![]() 求证:
求证:![]() .
.
![]() 将射线AE绕点A顺时针旋转
将射线AE绕点A顺时针旋转![]() 后,所得的射线与线段BD的延长线交于点F,连接CE.
后,所得的射线与线段BD的延长线交于点F,连接CE.
![]() 依题意补全图形;
依题意补全图形;
![]() 用等式表示线段EF,CE,BE之间的数量关系,并证明.
用等式表示线段EF,CE,BE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果把一条抛物线绕它的顶点旋转180°得到的抛物线我们称为原抛物线的“孪生抛物线”.
(1)求抛物线y=x-2x的“孪生抛物线”的表达式;
(2)若抛物线y=x-2x+c的顶点为D,与y轴交于点C,其“孪生抛物线”与y轴交于点,请判断△DCC’的形状,并说明理由:
(3)已知抛物线y=x-2x-3与y轴交于点C,与x轴正半轴的交点为A,那么是否在其“孪生抛物线”上存在点P,在y轴上存在点Q,使以点A、C、P、Q为顶点的四边形为平行四边形,若存在,求出P点的坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 .
(2)请用树状图或列表法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com