
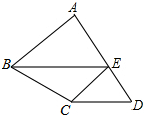
 如图,在四边形ABCD中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为3,△ECD的面积为1,则△BCE的面积是( )
如图,在四边形ABCD中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为3,△ECD的面积为1,则△BCE的面积是( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 由EC∥AB,EB∥DC,可得∠A=∠CED,∠AEB=∠D,证得△ABE与△ECD相似,由△ABE的面积为3,△CDE的面积为1,可得AB:CE=$\sqrt{3}$:1,又由EC∥AB,可得△ABE与△BCE等高,然后由等高三角形的面积比等于对应底的比,求得△BCE的面积.
解答 解:∵EC∥AB,
∴∠A=∠CED,
∵EB∥DC
∴∠AEB=∠D,
∴△ABE∽△ECD,
∴($\frac{BE}{CD}$)2=($\frac{AB}{CE}$)2=$\frac{{S}_{△ABE}}{{S}_{△ECD}}$=$\frac{3}{1}$=3,
∴$\frac{AB}{CE}$=$\sqrt{3}$,
∴AB=$\sqrt{3}$CE,
∵△ABE以AB为底边的高与△BCE以CE为底的高相等,
∴$\frac{{S}_{△ABE}}{{S}_{△BCE}}$=$\frac{AB}{CE}$=$\sqrt{3}$,
∴S△BCE=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
故选C.
点评 此题考查了相似三角形的判定与性质.注意相似三角形的面积比等于相似比的平方、等高三角形面积的比等于其对应底的比.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D,E分别是AB,AC的中点,CD=2DE,延长ED到点F,使得DF=CD,连接BF.
如图,在△ABC中,D,E分别是AB,AC的中点,CD=2DE,延长ED到点F,使得DF=CD,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 296瓶 | B. | 298瓶 | C. | 300瓶 | D. | 302瓶 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
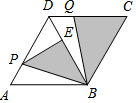 如图,菱形ABCD的边长为4,∠A=60°,点P是边AD上的动点,∠PBQ=60°,BQ交边CD于点Q,过点Q作BC的平行线交BD于点E.设AP=x时,图中两阴影部分面积的差为y(即y=S△BQC-S△BPE),则y与x之间的函数关系式是( )
如图,菱形ABCD的边长为4,∠A=60°,点P是边AD上的动点,∠PBQ=60°,BQ交边CD于点Q,过点Q作BC的平行线交BD于点E.设AP=x时,图中两阴影部分面积的差为y(即y=S△BQC-S△BPE),则y与x之间的函数关系式是( )| A. | $y=-\frac{{\sqrt{3}}}{4}{x^2}+\sqrt{3}$ | B. | $y=-\frac{{\sqrt{3}}}{2}{x^2}+2\sqrt{3}$ | C. | $y=-\frac{{\sqrt{3}}}{2}{x^2}+2\sqrt{3}x$ | D. | $y=-\frac{{\sqrt{3}}}{4}{x^2}+\sqrt{3}x$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
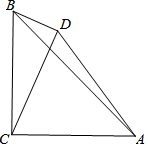 如图,在△ABC中,∠ACB=90°,AC=BC,D是△ABC外一点,连接AD、BD、CD,若∠CDB=90°,BD=3,AD=$\sqrt{65}$,则AC长为$\sqrt{58}$.
如图,在△ABC中,∠ACB=90°,AC=BC,D是△ABC外一点,连接AD、BD、CD,若∠CDB=90°,BD=3,AD=$\sqrt{65}$,则AC长为$\sqrt{58}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com