
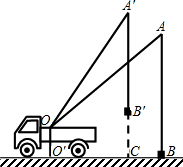
 小君同学在课外活动中观察吊车工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO′=2米,当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B 于点B,A′B′垂直地面O′B 于点C,吊臂长度OA′=OA=10米且cosA=0.6,∠A′=30°.
小君同学在课外活动中观察吊车工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO′=2米,当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B 于点B,A′B′垂直地面O′B 于点C,吊臂长度OA′=OA=10米且cosA=0.6,∠A′=30°.分析 此题首先把实际问题转化为解直角三角形问题来解决,(1)先过点O作OD⊥AB于点D,交A′C于点E,则得出EC=DB=OO′=2,ED=BC,通过解直角三角形AOD和A′OE得出OD与OE,从而求出BC.
(2)先解直角三角形A′OE,得出A′E,然后求出B′C.
解答  解:(1)过点O作OD⊥AB于点D,交A′C于点E
解:(1)过点O作OD⊥AB于点D,交A′C于点E
根据题意可知EC=DB=OO′=2米,ED=BC
∴∠A′ED=∠ADO=90°.
在Rt△AOD中,∵cosA=0.6,OA=10米,
∴AD=6米,
∴OD=8米.
在Rt△A′OE中,
∵sinA′=$\frac{1}{2}$,
OA′=10米
∴OE=5米.
∴BC=ED=OD-OE=8-5=3米.
(2)在Rt△A′OE中,
A′E=$\sqrt{A′{O}^{2}-O{E}^{2}}$=5$\sqrt{3}$米.
∴B′C=A′C-A′B′
=A′E+CE-AB
=A′E+CE-(AD+BD)
=5$\sqrt{3}$+2-(6+2)
=5$\sqrt{3}$-6(米).
答:此重物在水平方向移动的距离BC是3米,此重物在竖直方向移动的距离B′C是(5$\sqrt{3}$-6)米.
点评 此题考查了解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题来解决,本题运用了直角三角形函数及勾股定理.


科目:初中数学 来源: 题型:选择题
| A. | 1:1000000 | B. | 20:200 | C. | 1:10 | D. | 20000000:20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一个数值转换器,原理如图所示,若开始输入的值是5,可发现第1次输出的结果是16,第2次输出的结果是8,依次继续下去…,第101次输出的结果是( )
有一个数值转换器,原理如图所示,若开始输入的值是5,可发现第1次输出的结果是16,第2次输出的结果是8,依次继续下去…,第101次输出的结果是( )| A. | 1 | B. | 16 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>2 | B. | x<-$\frac{1}{2}$ | C. | -$\frac{1}{2}$<x<2 | D. | $\frac{1}{2}$<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com