
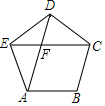
 如图,AD、EC是正五边形ABCDE的两条对角线,则$\frac{EF}{FC}$=$\frac{\sqrt{5}-1}{2}$.
如图,AD、EC是正五边形ABCDE的两条对角线,则$\frac{EF}{FC}$=$\frac{\sqrt{5}-1}{2}$. 分析 在正五边形ABCDE中,设EF=x,CF=y,首先证明CD=DE=CF=y,由△EDF∽△ECD,推出$\frac{DE}{EC}$=$\frac{EF}{ED}$,推出y2=x(x+y),即x2+xy-y2=0, 即($\frac{x}{y}$)2+($\frac{x}{y}$)-1=0,解方程即可解决问题.
即($\frac{x}{y}$)2+($\frac{x}{y}$)-1=0,解方程即可解决问题.
解答 解:在正五边形ABCDE中,设EF=x,CF=y,
∵∠EDA=∠EAD=∠DEC=∠DCE=36°,
∴∠CDF=∠CFD=72°,
∴CD=DE=CF=y,
又∵∠DEF=∠DEC,
∴△EDF∽△ECD,
∴$\frac{DE}{EC}$=$\frac{EF}{ED}$,
∴y2=x(x+y),
∴x2+xy-y2=0,
∴($\frac{x}{y}$)2+($\frac{x}{y}$)-1=0,
∴$\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$或$\frac{-1-\sqrt{5}}{2}$(舍弃),
∴$\frac{EF}{FC}$=$\frac{\sqrt{5}-1}{2}$.
故答案为$\frac{{\sqrt{5}-1}}{2}$;
点评 本题考查相似三角形的判定和性质、正五边形等知识,具体的规划是学会用参数解决问题,把问题转化为方程解决,属于中考常考题型,体现了数形结合的思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(9,2),那么能使y2>y1成立的x的取值范围是-2<x<9.
如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(9,2),那么能使y2>y1成立的x的取值范围是-2<x<9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )
如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.25≤a<4.35 | B. | 4.20≤a<4.40 | C. | 4.30≤a<4.35 | D. | 4.295≤a<4.305 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com