
A.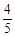 | B.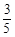 | C.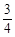 | D.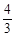 |
科目:初中数学 来源:不详 题型:解答题
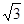 海里问此时是否需要向此未经特许的船只发出警告,命令其不得进入我国领海?
海里问此时是否需要向此未经特许的船只发出警告,命令其不得进入我国领海?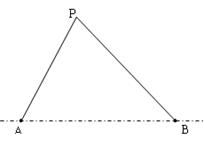
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
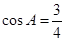 ,则下列结论正确的为 ( )
,则下列结论正确的为 ( )| A.0°<∠A < 30° | B.30°<∠A < 45° |
| C.45°< ∠A < 60° | D.60°< ∠A < 90° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
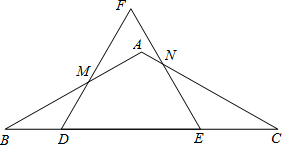
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,矩形ABCD的顶点A、B分别在边OM 、ON上运动,且形状和大小保持不变,其中AB=4,BC=3.
,矩形ABCD的顶点A、B分别在边OM 、ON上运动,且形状和大小保持不变,其中AB=4,BC=3.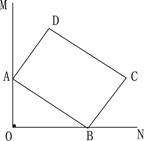
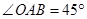 时,OA的长为 ;
时,OA的长为 ;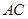 ∥
∥ 时,求OA的长;
时,求OA的长;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com