
分析 (1)首先把点A(1,b)代入直线y=$\frac{1}{2}$x+1求得b,再进一步代入抛物线y=ax2求得a即可;
(2)把二次函数与一次函数建立方程求得答案即可.
解答 解:(1)把点A(1,b)代入直线y=$\frac{1}{2}$x+1得b=$\frac{3}{2}$,
把点A(1,$\frac{3}{2}$)代入y=ax2求得a=$\frac{3}{2}$;
(2)由题意得:
$\frac{1}{2}$x+1=$\frac{3}{2}$x2,
解得:x1=1,x2=-$\frac{2}{3}$.
因此抛物线与直线的交点坐标为(1,$\frac{3}{2}$)和(-$\frac{2}{3}$,$\frac{2}{3}$).
点评 此题考查待定系数法求函数解析式,一次函数与二次函数的交点问题,掌握图象上点的坐标特征是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
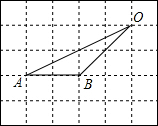 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )| A. | $\frac{10\sqrt{10}}{3}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程没有实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 无法判断方程实数根情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com