
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
分析 (1)频数=频率×总数,由第1组可得到样本容量,再计算第四组的频数和第五组的频率;
(2)共有50个数,那么中位数就是按顺序排列后第25个和第26个的平均数;
(3)应先算出样本中电费支出低于1400元的家庭占50个家庭的百分比,乘以30000即可.
解答 解:(1)a=50×0.200=10,b=5÷50=0.100,
如图所示: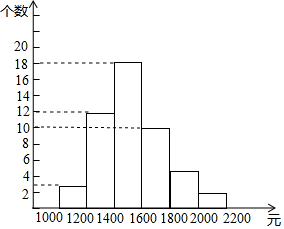
故答案为:10,0.100;
(2)由图中的数据可得,
总共有50个数据,中位数为第25个和第26个数的平均数,故中位数落在1400<x<1600;
(3)每年电费支出低于1400元的家庭数为(0.060+0.240)×30000=9000(个).
答:估计该地区有9000个一年电费支出低于1400元的家庭.
点评 本题考查了频数(率)分布直方图,频率和中位数的定义以及如何用样本估计总体.需注意:频数=频率×总数.


科目:初中数学 来源: 题型:解答题
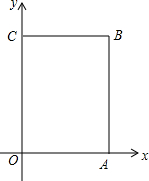 已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)
已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
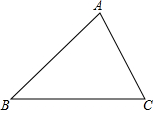 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有1对或2对 | B. | 只有1对 | C. | 只有2对 | D. | 有2对或3对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com