
分析 (1)根据两种收费方案,分别列出函数关系式即可;
(2)列出不等式即可解决问题;
(3)分别求出两种方案的购买量,即可判断;
解答 解:(1)按方案A:y=5.4x(1000≤x≤5000),
按方案B:y=5x+1000(1000≤x≤5000).
(2)由题意5.4x<5x+1000,
解得x<2500,
∵1000≤x≤5000,
∴购买量在1000≤x<2500时,选用方案A比方案B付款少.
(3)由5.4x=10000,解得x≈1852,
由5x+1000=10000,解得x=1800,
∵1852>1800,
∴选择方案A.
点评 本题考查一次函数的应用、一元一次不等式、一元一次方程等知识,解题的关键是学会构建函数、方程、不等式解决实际问题,属于中考常考题型.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
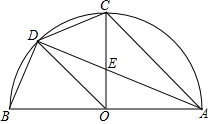 如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CE•CO,其中正确结论的序号是①②③.
如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CE•CO,其中正确结论的序号是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20a+17c=37ac | B. | (x2y)3=x5y3 | ||
| C. | x3÷x6=x3 | D. | (a+b-1)2=a2+b2+1+2ab-2a-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
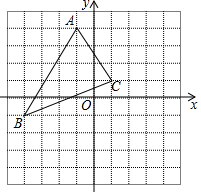 如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).
如图,在平面直角坐标系中,A(-1,4),B(-4,-1),C(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
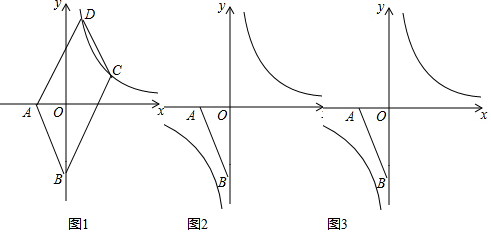
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com