练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．在Rt△ABC中，∠C=90°，那么下列关系中，正确的是（　　）
    A．c=a•sinAB．c=a•tanAC．c=$\frac{a}{cosA}$D．c=$\frac{a}{sinA}$

    分析 根据锐角三角函数的定义对各个选项进行判断即可．

    解答 解：∵sinA=$\frac{a}{c}$，
    ∴a=c•sinA，A错误；B错误；
    cosA=$\frac{b}{c}$，C错误，
    ∵sinA=$\frac{a}{c}$，
    ∴c=$\frac{a}{sinA}$，D正确，
    故选：D．

    点评 本题考查的是锐角三角函数的定义，在Rt△ABC中，∠C=90°，则sinA=$\frac{a}{c}$，cosA=$\frac{b}{c}$，tanA=$\frac{a}{b}$．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．如图，在平面直角坐标系中，点A在第二象限，以A为顶点的抛物线经过原点，与x轴负半轴交于点B，对称轴为直线x=-1，点C在抛物线上，且位于点A、B之间（C不与A、B重合）．若△ABC的周长为m，四边形AOBC的周长为m+2（用含m的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．现定义某种运算“⊕”，对任意两个实数a，b，都有a⊕b=4a-b2，例如1⊕2=4×1-22=0，请按上面定义的运算解答下面问题：
    （1）当a=2，b=4时，求2⊕4的值；
    （2）当a=x，b=3时，化简：x⊕3-3⊕x；
    （3）当a=x，b=6时，且x⊕6=x，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．2012年11月11日，某网站销售额191亿人民币．2014年，销售额增长到571亿人民币．设这两年销售额的平均增长率为x，则根据题意可列出方程191（1+x）2=571．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知x=$\frac{1}{\sqrt{3}+2}$，求x2-4x-4的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

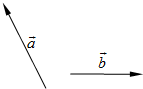    20．如图，已知平面内两个不平行的向量$\overrightarrow{a}$，$\overrightarrow{b}$，
    求作：$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$．（不要求写作法，但要保留作图痕迹，并写结论）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．A、B两地果园分别有苹果20吨和40吨，C．D两地分别需要苹果25吨和35吨；已知从A、B到C、D的运价如下表：
    到C地到D地
    A果园每吨12元每吨8元
    B果园每吨10元每吨9元
    （1）若从A果园运到C地的苹果为x吨，则从A果园运到D地的苹果为（20-x）吨，从A果园将苹果运往D地的运输费用为（160-8x）元．
    （2）用含x的式子表示出总运输费，请判断当x为何值时，总运输费最少，并求出此时的总运费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．若关于x的分式方程$\frac{x-2}{x-3}=\frac{m}{x-3}$有增根，则m的值是（　　）
    A．3B．2C．1D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

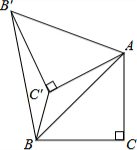    5．如图，已知△ABC中，∠C=90°，AC=BC=$\sqrt{2}$，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接B′B，则B′B的长为（　　）
    A．$\sqrt{2}$B．2C．2$\sqrt{2}$D．4

    查看答案和解析>>

    同步练习册答案