
 抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).
抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).分析 (1)根据抛物线与y轴的交点坐标求得c=3;根据对称轴为x=2来求b;
(2)抛物线C2与△OAB的边界总有两个公共点,即抛物线与线段OB有2个交点时,k的取值范围.
解答 解:(1)∵抛物线$y=\frac{1}{2}{x^2}+bx+c$与y轴交于点C(0,3),
∴c=3.
∵抛物线$y=\frac{1}{2}{x^2}+bx+c$的对称轴为x=2,
∴$-\frac{b}{{2×\frac{1}{2}}}=2$,
解得b=-2,
∴抛物线C1的解析式为$y=\frac{1}{2}{x^2}-2x+3$.
(2)由题意,抛物线C2的解析式为$y=\frac{1}{2}{x^2}+k$. 
当抛物线经过点A(2,0)时,$\frac{1}{2}×{2^2}+k=0$,
解得k=-2.
∵O(0,0),B(2,2),
∴直线OB的解析式为y=x.
由$\left\{\begin{array}{l}y=x\\ y=\frac{1}{2}{x^2}+k\end{array}\right.$,
得x2-2x+2k=0,①
当△=(-2)2-4×1×2k=0,即$k=\frac{1}{2}$时,
抛物线C2与直线OB只有一个公共点,
此时方程①化为x2-2x+1=0,
解得x=1,
即公共点P的横坐标为1,点P在线段OB上.
∴k的取值范围是$-2<k<\frac{1}{2}$.
点评 本题考查了二次函数图象与几何变换.解答(2)时,利用了“数形结合”的数学思想,使比较抽象的问题变得直观化,降低了解题的难度.


科目:初中数学 来源: 题型:解答题
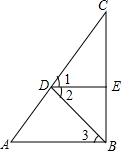 如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 82分、83分 | B. | 83分、89分 | C. | 91分、72分 | D. | 91分、83分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数)
我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com