
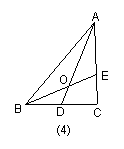
在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下事实: 如图1,当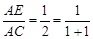 时,有
时,有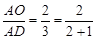 ;
;
如图2,当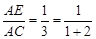 时,有
时,有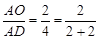 ;
;
如图3,当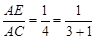 时,有
时,有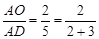 ;在图4中,当
;在图4中,当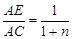 时,
时,
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.
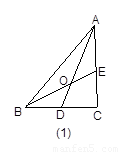
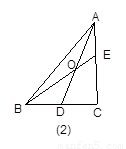
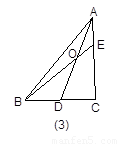
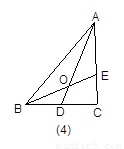
科目:初中数学 来源:2011-2012学年重庆市八年级下学期期末考试(二)数学试卷(带解析) 题型:解答题
在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下事实: 如图1,当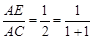 时,有
时,有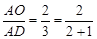 ;
;
如图2,当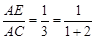 时,有
时,有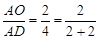 ;
;
如图3,当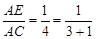 时,有
时,有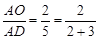 ;在图4中,当
;在图4中,当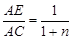 时,
时,
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.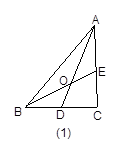
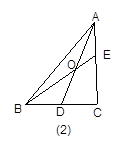

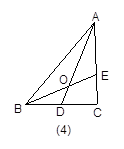
查看答案和解析>>
科目:初中数学 来源: 题型:
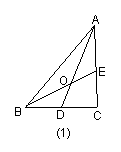
在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下事实: 如图1,当![]() 时,有
时,有![]() ;
;
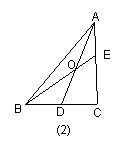
如图2,当![]() 时,有
时,有![]() ;
;
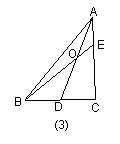
如图3,当![]() 时,有
时,有![]() ;在图4中,当
;在图4中,当![]() 时,
时,
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
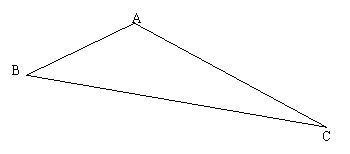
如图,在△ABC中,∠BAC为钝角,完成下列作图:
(1)作∠BAC的平分线AD;
(2)作AC边上的中线BE;
(3)作AB边上的高CF,AC边上的高BG.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com