
 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.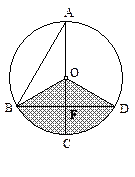
|
 AB=2
AB=2 .····················· 1分
.····················· 1分
 AEO中,∠BAC=30°,cos30°=
AEO中,∠BAC=30°,cos30°= .
. =
= =4. …………………………2分
=4. …………………………2分 .
. =
= .································································· 4分
.································································· 4分
|
 . ∴∠BAD=2∠BAC=60°,
. ∴∠BAD=2∠BAC=60°, AB=2
AB=2 ,sin60°=
,sin60°= ,AF=AB·sin60°=4
,AF=AB·sin60°=4 ×
× =6.
=6. .∴OB=4. ···························· 3分
.∴OB=4. ···························· 3分 S圆=
S圆= . ········································································ 4分
. ········································································ 4分
 ,∴
,∴ . ……………………2分
. ……………………2分 π·OA2=
π·OA2= ×42·π=
×42·π= .……………………4分
.……………………4分 . ∴
. ∴ . ···················································· 6分
. ···················································· 6分 <8
<8 -12,故能得到两个这样的底面。……………………8分
-12,故能得到两个这样的底面。……………………8分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

| A.DE="DO" | B.AB=AC |
| C.CD="DB" | D.AC∥OD |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,
图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3, 线于点M.
线于点M.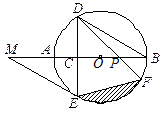
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com