
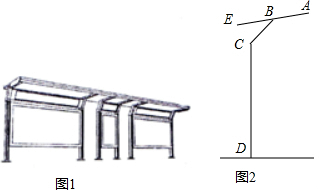
分析 由于横梁一端点E在支柱DC的延长线上,所以延长DC交直线AB于点E,可得∠EBC=45°,∠ECB=30°.过点E作EP⊥BC.构建等腰直角三角形,通过解直角三角形得到CE的长度即可.
解答 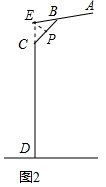 解:如图,延长DC交直线AB于点E,过点E作EP⊥BC,则可得∠EBC=45°,∠ECB=30°.
解:如图,延长DC交直线AB于点E,过点E作EP⊥BC,则可得∠EBC=45°,∠ECB=30°.
在Rt△BPE中,EP=BE•sin∠EBP=0.35×sin45°≈0.25m.
在Rt△CPE中,∵∠ECP=30°,
∴EC=2EP≈0.5m.
点评 本题考查了直角三角形的应用,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
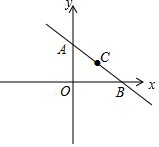 如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).
如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com