
 ,若cos
,若cos =
=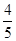 ,OC =" 15" ,求AB的长。
,OC =" 15" ,求AB的长。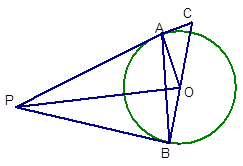
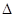 COA
COA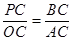 即AC?PC= OC?BC
即AC?PC= OC?BC =
=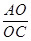 =
=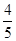 ∴AO=12
∴AO=12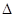 COA ∠BPC=∠AOC=
COA ∠BPC=∠AOC=
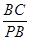 =
=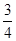 ∴PB=36 PO=12
∴PB=36 PO=12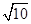
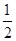 AB?PO= OB?BP ∴AB=
AB?PO= OB?BP ∴AB=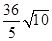
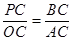 ,即AC?PC= OC?BC;
,即AC?PC= OC?BC;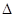 COA求出PB=36,OP=12
COA求出PB=36,OP=12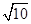 ;然后由切线的性质求AB的长.
;然后由切线的性质求AB的长.

科目:初中数学 来源:不详 题型:填空题
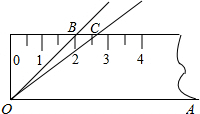
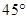 的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将
的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将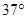 的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm
的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm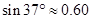 ,
,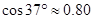 ,
,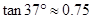 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.h≤17cm | B.h≥8cm | C.15cm≤h≤16cm | D.7cm≤h≤16cm |
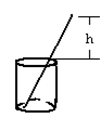
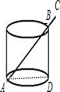
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 。请计算停车位所占道路的宽度EF(结果精确到0.1米)。
。请计算停车位所占道路的宽度EF(结果精确到0.1米)。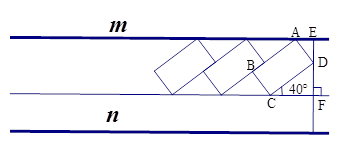
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
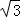 )、D(0,3
)、D(0,3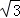 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.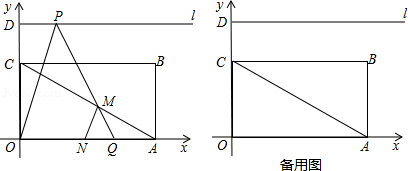
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com