
分析 可先把抛物线解析式化为顶点式,容易确定出开口方向、对称轴及顶点坐标,再利用描点法可画出其图象.
解答 解:(1)∵y=-3x2+12x-3=-3(x-2)2+9,
∴抛物线开口向下,对称轴为x=2,顶点坐标为(2,9),
其图象如图1所示;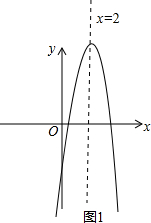
(2)∵y=4x2-24x+26=4(x-3)2-10,
∴抛物线开口向上,对称轴为x=3,顶点坐标为(3,-10);
其图象如图2所示;
(3)∵y=2x2+8x-6=2(x+2)2-14,
∴抛物线开口向上,对称轴为x=-2,顶点坐标为(-2,-14);
其图象如图3所示;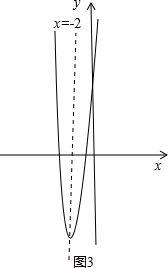
(4)∵y=$\frac{1}{2}$x2-2x-1=$\frac{1}{2}$(x-2)2-3,
∴抛物线开口向上,对称轴为x=2,顶点坐标为(2,-3);
其图象如图4所示;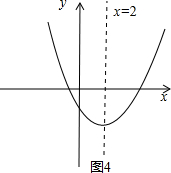
点评 本题考查了抛物线对称轴和抛物线的顶点坐标的求法,以及用描点法画函数图象,是基础知识,比较简单.


科目:初中数学 来源: 题型:选择题
| A. | 5千米 | B. | 7千米 | C. | 8千米 | D. | 9千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 打开电视,正在播放动画片 | |
| C. | 3个人分成两组,一定有2个人分在一组 | |
| D. | 随意掷两个均匀的骰子,上面的点数之和为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-2) | B. | (-2,-6) | C. | (2,2) | D. | (2,2)或(-2,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
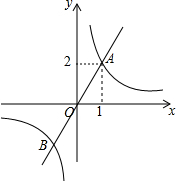 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | -1<x<0或x>1 | B. | x<-1或0<x<1 | C. | x>1 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
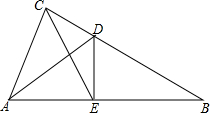
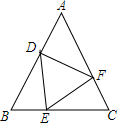 已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.
已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com