
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上运动,且
轴的正半轴上运动,且![]() ,下列结论:
,下列结论:
①![]()
②当![]() 时四边形
时四边形![]() 是正方形
是正方形
③四边形![]() 的面积和周长都是定值
的面积和周长都是定值
④连接![]() ,
,![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
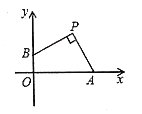
A.①②B.①②③C.①②④D.①②③④
【答案】A
【解析】
过P作PM⊥y轴于M,PN⊥x轴于N,易得出四边形PMON是正方形,推出OM=OM=ON=PN=2,证得△APM≌△BPN,可对①进行判断,推出AM=BN,求出OA+OB=ON+OM=4,当OA=OB时,OA=OB=2,然后可对②作出判断,由△APM≌△BPN可对四边形OAPB的面积作出判断,由OA+OB=4,然后依据AP和PB的长度变化情况可对四边形OAPB的周长作出判断,求得AB的最大值以及OP的长度可对④作出判断.
过P作PM⊥y轴于M,PN⊥x轴于N,
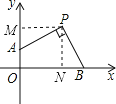
∵P(2,2),
∴PN=PM=2.
∵x轴⊥y轴,
∴∠MON=∠PNO=∠PMO=90°,
则四边形MONP是正方形,
∴OM=ON=PN=PM=2,
∵∠MPN=∠APB=90°,
∴∠MPA=∠NPB.
在△MPA≌△NPB中,
 ,
,
∴△MPA≌△NPB,
∴PA=PB,故①正确.
∵△MPA≌△NPB,
∴AM=BN,
∴OA+OB=OA+ON+BN=OA+ON+AM=ON+OM=2+2=4.
当OA=OB,即OA=OB=2时,
则点A、B分别与点M、N重合,此时四边形OAPB是正方形,故②正确.
∵△MPA≌△NPB,
∴![]() .
.
∵OA+OB=4,PA=PB,且PA和PB的长度会不断的变化,故周长不是定值,故③错误.
∵∠AOB+∠APB=180°,
∴点A、O、B、P共圆,且AB为直径,所以AB≥OP,故④错误.
故选:A.


科目:初中数学 来源: 题型:
【题目】学校开设“慈善基金”活动以来,受到同学们的广泛帮助,学校为了解全校学生捐款的情况,随机调查了部分学生的捐款金额,并制成如图不完整的统计图表.
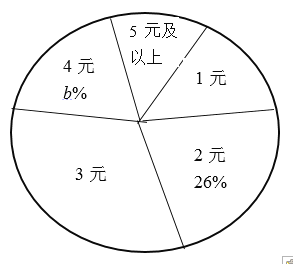
捐款金额 | 1元 | 2元 | 3元 | 4元 | 5元及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)请计算扇形统计图中的3元所对应的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,统计该校学生在5元及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点![]() 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点![]() 叫做 “整点”.例如:
叫做 “整点”.例如:![]() 、
、![]() 都是“整点”,抛物线
都是“整点”,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 两点,若该抛物线在
两点,若该抛物线在![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域(包括边界)恰有七个整点,则
所围成的区域(包括边界)恰有七个整点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对“隔离直线”给出如下定义:点
中,对“隔离直线”给出如下定义:点![]() 是图形
是图形![]() 上的任意一点,点
上的任意一点,点![]() 是图形
是图形![]() 上的任意一点,若存在直线
上的任意一点,若存在直线![]() :
:![]() 满足
满足![]() 且
且![]() ,则称直线
,则称直线![]() :
:![]() 是图形
是图形![]() 与
与![]() 的“隔离直线”,如图
的“隔离直线”,如图![]() ,直线
,直线![]() :
:![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的一条“隔离直线”.
的一条“隔离直线”.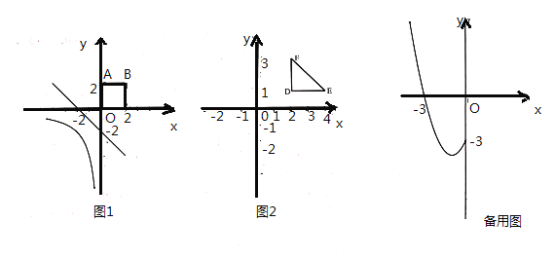
(1)在直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是图
中,是图![]() 函数
函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”的为 .
的“隔离直线”的为 .
(2)如图![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的两腰分别与坐标轴平行,直角顶点
的两腰分别与坐标轴平行,直角顶点![]() 的坐标是
的坐标是![]() ,⊙O的半径为
,⊙O的半径为![]() ,是否存在
,是否存在![]() 与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
(3)正方形![]() 的一边在
的一边在![]() 轴上,其它三边都在
轴上,其它三边都在![]() 轴的左侧,点
轴的左侧,点![]() 是此正方形的中心,若存在直线
是此正方形的中心,若存在直线![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”,请直接写出
的“隔离直线”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,将线段
轴的正半轴上,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() .
.
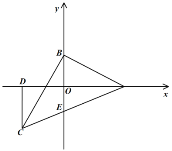
(1)当点![]() 在第三象限时,求实数
在第三象限时,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,设![]() ,当
,当![]() 取得最大值时,求图象经过
取得最大值时,求图象经过![]() 两点的二次函数
两点的二次函数![]() 的解析式;
的解析式;
(3)在(2)的条件下,将直线![]() 向上平移
向上平移![]() 个单位后与二次函数
个单位后与二次函数![]() 的图象交点的横坐标为
的图象交点的横坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
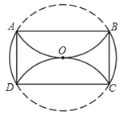
【题目】如图,在⊙O中,分别将弧AB、弧CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
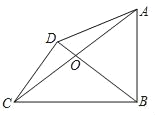
【题目】如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com