
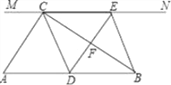
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【答案】(1)证明见解析;(2)当点D是AB中点时,四边形BECD是菱形,理由见解析;(3)当∠A的大小是45°时,四边形BECD是正方形.
【解析】分析:(1)由BC⊥AC,DE⊥BC,得到DE∥AC,从而判断出四边形ADEC是平行四边形.即可,
(2)先判断出△BFD≌△CFE,再判断出BC和DE垂直且互相平分,得到四边形BECD是菱形.
(3)先判断出∠CDB=90°,从而得到有一个角是直角的菱形是正方形.
解析:(1)证明:∵直线m∥AB,
∴EC∥AD.
又∵∠ACB=90°,
∴BC⊥AC.
又∵DE⊥BC,
∴DE∥AC.
∵EC∥AD,DE∥AC,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)当点D是AB中点时,四边形BECD是菱形.
证明:∵ D是AB中点,
∴DB=DA
又∵直线m∥AB,CE=AD
∴DB= CE,DB ∥ CE
∴四边形BDCE是平行四边形
又∵DE⊥BC
∴四边形BECD是菱形
(3)当∠A的大小是45°时,四边形BECD是正方形.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
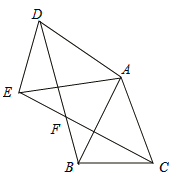
(1)求证:![]() ;
;
(2)若AB=2,![]() ,当四边形ADFC是菱形时,求BF的长。
,当四边形ADFC是菱形时,求BF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
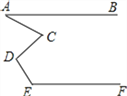
A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查方式的是()
A. 调查某水库中鱼的种类
B. 调查某市市民对汽车废气污染环境的看法
C. 调查某班同学的视力情况
D. 调查某型号节能灯的使用寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)完成下面的推理说明:
已知:如图,![]() ∥
∥![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() .
.

求证:![]() ∥
∥![]() .
.
证明:![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() (已知),
(已知),
![]() ,
,![]() ( ).
( ).
![]() ∥
∥![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() (等式的性质).
(等式的性质).
![]() ∥
∥![]() ( ).
( ).
(2)说出(1)的推理中运用了哪两个互逆的真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛掷一枚质地均匀、六个面上分别刻有点数1~6的正方体骰子2次,则“向上一面的点数之和为10”是( )
A. 必然事件B. 不可能事件C. 确定事件D. 随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
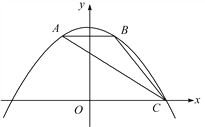
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com