
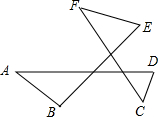
 如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.
如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度. 分析 利用三角形外角性质可得∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,三式相加易得∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,而∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,从而可求∠A+∠B+∠C+∠D+∠E+∠F.
解答  解:如右图所示,
解:如右图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
点评 本题考查了三角形内角和定理.解题的关键是三角形内角和定理与三角形外角性质的联合使用,知道三角形的外角和等于360°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC
(1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
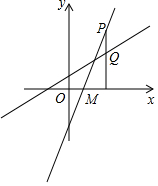 如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.
如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com