
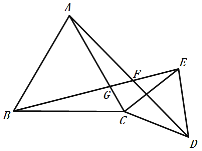
【题目】如图,△ABC和△CDE都是等边三角形,连接AD、BE,AD与BE交于点F.
(1)求证AD=BE;
(2)∠BFA= °.

【答案】(1)证明见解析;(2)60.
【解析】
(1)△ABC和△CDE都是等边三角形,根据等边三角形的性质,利用SAS可证得△ACD≌△BCE,从而证得结果;
(2)在![]() 和
和![]() 中,利用(1)的结论结合对顶角相等,可求得答案.
中,利用(1)的结论结合对顶角相等,可求得答案.
(1)∵△ABC和△CDE都是等边三角形,
∴AC=BC, CD=CE,∠ACB=∠ECD=60°.
∴∠ACB+∠ACE=∠ECD+∠ACE, 即∠ACD=∠BCE.
在△ACD和△BCE中,
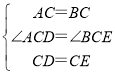
∴△ACD≌△BCE(SAS).
∴AD=BE.
(2)∵△ACD≌△BCE
∴∠CAD=∠CBE
在![]() 和
和![]() 中,
中,
∠GAF=∠GBC
∠AGF=∠BGC(对顶角相等)
∴∠BFA=∠ACB=60![]()
故答案为:60.


科目:初中数学 来源: 题型:
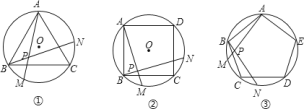
【题目】如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.如图①、②、③,正三角形
上逆时针运动.如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.
上逆时针运动.
(1)求图①中![]() 的度数;
的度数;
(2)图②中,![]() 的度数是________,图③中
的度数是________,图③中![]() 的度数是________;
的度数是________;
(3)根据前面探索,你能否将本题推广到一般的正![]() 边形情况?若能,写出推广问题和结论;若不能,请说明理由.
边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“古圣先贤孝为宗,万善之门孝为基,礼敬尊亲如活佛,成就生命大意义,父母恩德重如山,知恩报恩不忘本,做人饮水要思源,才不愧对父母恩…”.某实验中学为加强对学生的感恩教育,教学生唱《跪羊图》,并对学生的学习成果进行随机抽查,现对部分学生的成绩(x为整数,满分100分)进行了统计,绘制了如下尚不完整的统计图表.
组别 | 成绩分组 (单位:分) | 频数 | 频率 |
A |
| 40 | 0.1 |
B |
| 60 | c |
C |
| a | 0.2 |
D |
| 160 | 0.4 |
E |
| 60 | 0.15 |
合计 | b | 1 |
调查结果扇形统计图

根据以上信息解答下列问题:/p>
(1)统计表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)求扇形统计图中D组所在扇形的圆心角的度数;
(3)若参加《跪羊图》演唱的同学共有2000人,请估计成绩在90分及以上的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
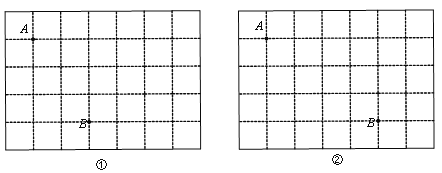
【题目】如图①、图②,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点,图①和图②中的点A、点B都是格点.分别在图①、图②中画出格点C,并满足下面的条件:
(1)在图①中,使∠ABC=90°.此时AC的长度是 .
(2)在图②中,使AB=AC.此时△ABC的边AB上的高是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:

如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com