
分析 本题可转化为解不等式组的问题,求出无解的不等式即可.
解答 解:由题意可得:
$\left\{\begin{array}{l}{1+a>0}\\{1-a>0}\end{array}\right.$
$\left\{\begin{array}{l}{1+a<0}\\{1-a<0}\end{array}\right.$,、
$\left\{\begin{array}{l}{1+a>0}\\{1-a<0}\end{array}\right.$、
$\left\{\begin{array}{l}{1+a<0}\\{1-a>0}\end{array}\right.$,
解这四组不等式可知$\left\{\begin{array}{l}{1+a<0}\\{1-a>0}\end{array}\right.$无解,
因而点A的横坐标是负数,纵坐标是正数,不能同时成立,即点A一定不在第二象限,
故答案为二.
点评 本题主要考查平面直角坐标系中各象限内点的坐标的符号,把符号问题转化为解不等式组的问题.


科目:初中数学 来源: 题型:解答题
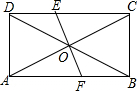 如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.
如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
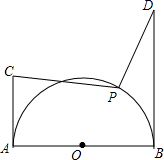 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.
如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
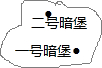 如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.
如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com