
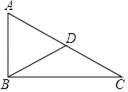
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题意作图即可;
(2)先根据BD为AC边上的中线,AD=DC,再证明△ABD≌△CED(AAS)得AB=EC,已知∠ABC=90°即可得四边形ABCE是矩形.
(1)解:如图所示:E点即为所求;
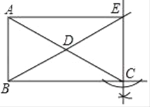
(2)证明:∵CE⊥BC,
∴∠BCE=90°,
∵∠ABC=90°,
∴∠BCE+∠ABC=180°,
∴AB∥CE,
∴∠ABE=∠CEB,∠BAC=∠ECA,
∵BD为AC边上的中线,
∴AD=DC,
在△ABD和△CED中
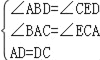 ,
,
∴△ABD≌△CED(AAS),
∴AB=EC,
∴四边形ABCE是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCE是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.


备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为_____m(结果保留一位小数,参考数据:sin53°≈![]() , cos53°≈
, cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:材料1:如果一个多项式中的字母按照任何次序轮换后,原多项式不变,那么称该多项式是轮换多项式,简称轮换式.例如:多项式![]() ,将字母
,将字母![]() 换字母
换字母![]() ,字母
,字母![]() 换字母
换字母![]() ,得到多项式
,得到多项式![]() ,而
,而![]() ,所以多项式
,所以多项式![]() 是轮换式.我们把含有两个字母的轮换式称为二元轮换式,其中含字母
是轮换式.我们把含有两个字母的轮换式称为二元轮换式,其中含字母![]() ,
,![]() 的二元轮换式的基本轮换式是
的二元轮换式的基本轮换式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等二元轮换式都可以用
等二元轮换式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
材料2:因为![]() ,所以,对于二次项系数为1的二次三项式
,所以,对于二次项系数为1的二次三项式![]() 的因式分解,就是把常数项
的因式分解,就是把常数项![]() 分解成两个数的积,且使这两数的和等于
分解成两个数的积,且使这两数的和等于![]() ,即如果有
,即如果有![]() ,
,![]() 两数满足
两数满足![]() ,
,![]() ,则有
,则有![]() .如分解因式
.如分解因式![]() :因为
:因为![]() ,
,![]() ,所以
,所以![]() .
.
请根据以上材料解决下列问题:
(1)式子①![]() ;②
;②![]() ;③
;③![]() ,④
,④![]() 中,属于轮换式的是 (填序号);
中,属于轮换式的是 (填序号);
(2)因式分解:![]() ;
;![]() ;
;
(3)若![]() (其中
(其中![]() ),且
),且![]() ,求
,求![]() 的值并把式子
的值并把式子![]() 因式分解.
因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
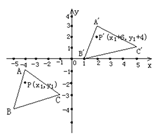
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,CD=CB,点E为BD的中点,且EA=EC,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=![]() AC;
AC;
(2)求线段AM、DM、BC之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com