
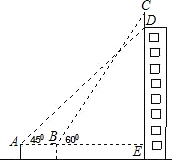
 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数) 科目:初中数学 来源: 题型:解答题
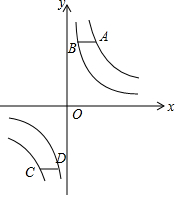 如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).
如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )| A. | (1,$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
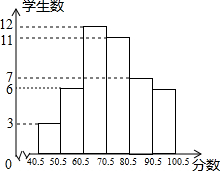 某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.
某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
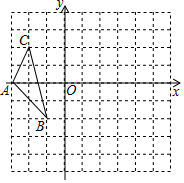 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
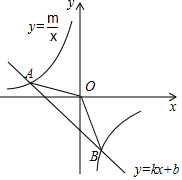 如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,
甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com