
【题目】根据下面给出的数轴,解答下面的问题:
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图 1,射线 OC在∠AOB的内部,图中共有 3个角:∠AOB、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线 OC是∠AOB的奇妙线.
(1)一个角的角平分线_______这个角的奇妙线.(填是或不是);
(2)如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).
① 当 t为何值时,射线 PM是∠QPN 的奇妙线?

②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转,并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,直线a与直线b交于点O,△ABC的顶点均在格点上.
(1)△ABC向右平移 个单位长度到△A1B1C1位置;
(2)对△ABC分别作下列变换:
① 画出△ABC关于直线a对称的△A2B2C2;
② 将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 与△ 成轴对称,对称轴是直线 ;
② △ 与△ 成中心对称,并在图中标出对称中心D的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数![]() ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.
(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|-![]() +0.8|=____________;
+0.8|=____________;
(3)|![]() |=__________;
|=__________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-|-
|-|-![]() |-
|-![]() ×|-
×|-![]() |+
|+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①![]() ,②
,②![]() ,③
,③![]() 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.

(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
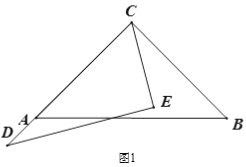
【题目】已知将一副三角板(直角三角板ABC和直角三角板CDE,∠ACB=90°,∠ECD=60°)如图1摆放,点D、A、C在一条直线上,将直角三角板CDE绕点C逆时针方向转动,变化摆放如图位置.
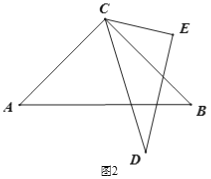
(1) 如图2,当∠ACD为多少度时,CB恰好平分∠ECD?
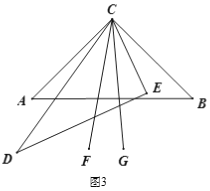
(2) 如图3,当三角板CDE摆放在∠ACB内部时,作射线CF平分∠ACE,射线CG平分∠BCD,如果三角形CDE在∠ACB内绕点C任意转动,∠FCG的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
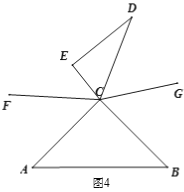
(3) 如图4,当三角板CDE转到∠ACB外部时,射线CF、CG仍然分别平分∠ACE、∠BCD,在旋转过程中,(2)中的结论是否成立?如果结论成立,请说明理由;如果不成立,请写出你的结论并根据图4说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
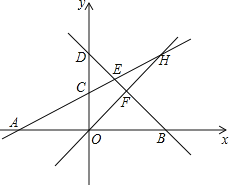
【题目】如图,直线AC:y=![]() x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.
x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.
(1)求直线BD的解析式和E的坐标.
(2)若直线y=x分别与直线AC,BD交于点H和F,求四边形ECOF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com