
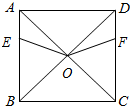
 ��֪������ABCD��AB=8����E��F�ֱ�ӵ�A��Dͬʱ��������ÿ��1m���ٶȷֱ������߶�AB��DC���B��C������˶������˶�ʱ��Ϊt��
��֪������ABCD��AB=8����E��F�ֱ�ӵ�A��Dͬʱ��������ÿ��1m���ٶȷֱ������߶�AB��DC���B��C������˶������˶�ʱ��Ϊt������ ��1�����������ε����ʵó�OA=OD����EAO=��FDO=45�㣬���AE=DF=t������SAS�Ƴ���EAO�ա�FDO���ɣ�
��2�����ӳ�EO��DC��M�������AOE�ա�COM������ȫ�������ε����ʵó�AE=CM=t������S=S�ı���AEMF-S��FOM������ɣ�
�ڸ���ȫ�ȵó�OE=OM�����S��EOF=$\frac{1}{2}$S��EFM=16-4t�����ɵó�����16-4t=$\frac{1}{3}$��16��������ɣ�
��� ��1��֤�������ı���ABCD�������Σ�
��OA=OD����EAO=��FDO=45�㣬
�ߵ�E��F�ֱ�ӵ�A��Dͬʱ��������ÿ��1m���ٶȷֱ������߶�AB��DC���B��C������˶������˶�ʱ��Ϊt��
��AE=DF=t��
�ڡ�EAO�͡�FDO��
$\left\{\begin{array}{l}{OA=OD}\\{��EAO=��FDO}\\{AE=DF}\end{array}\right.$
���EAO�ա�FDO��SAS����
��OE=OF��
��2���⣺��S�Ĵ�С���������˶�ʱ��Ϊt�ı仯���仯��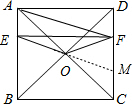
�����ǣ��ӳ�EO��DC��M��
��M��FC��ʱ��
���ı���ABCD�������Σ�
���OAE=��MCO=45�㣬OA=OC��
�ڡ�AOE�͡�COM��
$\left\{\begin{array}{l}{��EAO=��MCO}\\{AO=CO}\\{��AOE=��COM}\end{array}\right.$
���AOE�ա�COM��ASA����
��AE=CM=t��
��S=S�ı���AEMF-S��FOM
=$\frac{1}{2}$��t+8-t-t��•8-$\frac{1}{2}$����8-t-t��•4
=16��
��M��FD��ʱ��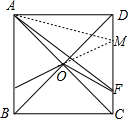
S=��AOE+S��AOF
=S��COM+S��AOF
=$\frac{1}{2}$S��AMC+$\frac{1}{2}$S��AFC=$\frac{1}{2}$��$\frac{1}{2}$��t��8+$\frac{1}{2}��\frac{1}{2}$��8-t����8=16��
����S�Ĵ�С���������˶�ʱ��Ϊt�ı仯���仯��
�ڡߡ�AOE�ա�COM��
��OE=OM��
��S��EOF=S��FOM=$\frac{1}{2}$S��EFM=$\frac{1}{2}$��$\frac{1}{2}$��8-t-t��•8=16-4t��
�ߡ�OEF�����ǡ�õ��ڵ�$\frac{1}{3}$S��
��16-4t=$\frac{1}{3}$��16��
��ã�t=$\frac{8}{3}$��
���ݶԳ��Կ�֪��t=$\frac{16}{3}$sʱ��Ҳ����������
�����˶�ʱ��ΪtΪ$\frac{8}{3}$s��$\frac{16}{3}$sʱ����OEF�����ǡ�õ��ڵ�$\frac{1}{3}$S��
���� ���⿼���������ε����ʣ�ȫ�������ε����ʺ��ж��������ε������Ӧ�ã����ۺ�����֪ʶ����������ǽ����Ĺؼ����ۺ��ԱȽ�ǿ���Ѷ�ƫ��


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
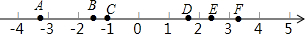
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
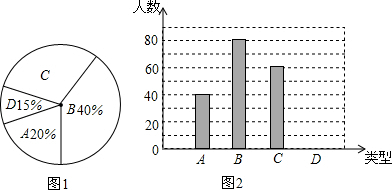
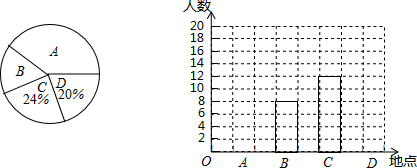
| A�� | ����ͳ��ͼ | B�� | ����ͳ��ͼ | C�� | ����ͳ��ͼ | D�� | Ƶ���ֲ�ֱ��ͼ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ѡ���У�����ͨ������ĵ����������� | |
| B�� | ����6��4��2��2��1��ƽ������3 | |
| C�� | ����3��5��4��1��-2�������3 | |
| D�� | �����ӻ�������һ�����ڲ���桱�DZ�Ȼ�¼� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | ʱ��t��Сʱ�� | ���� |
| A | t��0.5 | 5 |
| B | 0.5��t��1 | m |
| C | 1��t��1.5 | n |
| D | 1.5��t��2 | 30 |
| E | t��2 | 10 |
 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x2y2��2x-1�� | B�� | 3xy��2x-1�� | C�� | xy2��2x-1�� | D�� | xy��2x-1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com