
【题目】综合与实践
问题情境:在综合与实践课上,老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动,如图1,三角板![]() 和三角板
和三角板![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,连接
上,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.试判断线段
的中点.试判断线段![]() 与
与![]() 的数量关系和位置关系.
的数量关系和位置关系.
探究展示:勤奋小组发现,![]() ,
,![]() .并展示了如下的证明方法:
.并展示了如下的证明方法:
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .(依据1)
.(依据1)
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .(依据2)
.(依据2)
∴![]() .∴
.∴![]() .
.
反思交流:
(1)①上述证明过程中的“依据1”,“依据2”分别是指什么?
②试判断图1中,![]() 与
与![]() 的位置关系,请直接回答,不必证明;
的位置关系,请直接回答,不必证明;
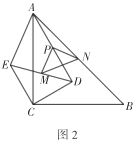
(2)创新小组受到勤奋小组的启发,继续进行探究,把![]() 绕点
绕点![]() 逆时针方向旋转到如图2的位置,发现
逆时针方向旋转到如图2的位置,发现![]() 是等腰直角三角形,请你给出证明;
是等腰直角三角形,请你给出证明;
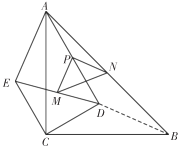
(3)缜密小组的同学继续探究,把![]() 绕点
绕点![]() 在平面内自由旋转,当
在平面内自由旋转,当![]() ,
,![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
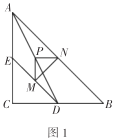
【答案】(1)①依据1:三角形的中位线平行于第三边并且等于第三边的一半.
依据2:直角三角形的两个锐角互余.②![]() . (2)见解析 (3)
. (2)见解析 (3)![]()
【解析】
(1)①根据三角形的中位线的性质和直角三角形的性质,即可得到答案;
②由![]() ,得∠ANP=45°,结合∠PNM=45°,即可得到结论;
,得∠ANP=45°,结合∠PNM=45°,即可得到结论;
(2)连接![]() ,先证
,先证![]() ,得
,得![]() ,
,![]() ,从而得
,从而得![]() 是等腰三角形.通过三角形外角的性质和直角三角形的性质可得
是等腰三角形.通过三角形外角的性质和直角三角形的性质可得![]()
![]() ,进而得
,进而得![]() ,即可得到结论;
,即可得到结论;
(3)由![]() 是等腰直角三角形,
是等腰直角三角形,![]() 可得,当BD最大时,
可得,当BD最大时,![]() 面积最大,进而即可得到答案.
面积最大,进而即可得到答案.
(1)①依据1:三角形的中位线平行于第三边并且等于第三边的一半.
依据2:直角三角形的两个锐角互余.
②![]() .理由如下:
.理由如下:
由勤奋小组发现,![]() ,
,![]() ,可知:PMN是等腰直角三角形,
,可知:PMN是等腰直角三角形,
∴∠PNM=45°,
∵![]() ,
,
∴∠ANP=∠B=45°,
∴∠ANM=45°+45°=90°,即:![]() ;
;
(2)连接![]() ,由旋转的性质知,
,由旋转的性质知,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中位线,
的中位线,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
又∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(3)由(2)知,![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
∴BD最大时,![]() 面积最大,此时,点
面积最大,此时,点![]() 在
在![]() 的延长线上,即:
的延长线上,即:![]() ,
,
∴PM的最大值为7,
∴![]() 的最大值
的最大值![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
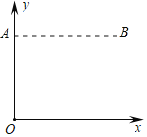
【题目】某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间(不包括A、B两点)经过时,将触发报警.现将A、B两点放置于平面直角坐标系![]() 中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线
中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线![]() (
(![]() <0)运动.若小车在运动过程中触发两次报警装置,则
<0)运动.若小车在运动过程中触发两次报警装置,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
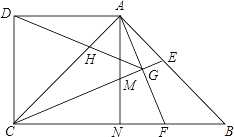
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.
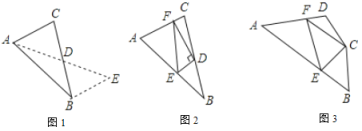
(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
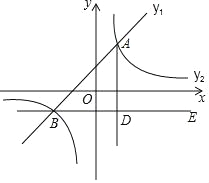
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
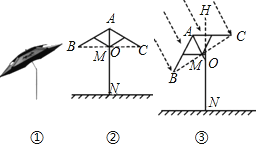
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
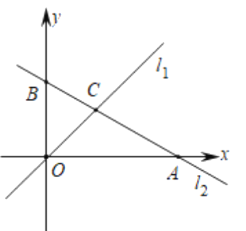

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com