
| 品牌 | 月租费 | 本地话费(元/分钟) | 长途话费(元/分钟) |
| 全球通 | 13元 | 0.35 | 0.15 |
| 神州行 | 0元 | 0.60 | 0.30 |
分析 设小明打长途电话的时间为x分钟,则打本地电话的时间为2x分钟,根据表格中计费规则分别表示出全球通和神州行所需的总费用,再分类讨论求得x的范围,结合“每月总通话时间在65~70分钟之间“可得答案.
解答 解:设小明打长途电话的时间为x分钟,则打本地电话的时间为2x分钟,
∴选择“全球通”所需总费用为13+0.15x+0.35×2x=0.85x+13,
选择“神州行”所需总费用为0.3x+0.6×2x=1.5x,
当0.85x+13>1.5x,即0<x<20时,选择神州行较为省钱;
当0.85x+13=1.5x,即x=20时,都一样省钱;
当0.85x+13<1.5x,即x>20时,选择全球通较为省钱;
∵每月总通话时间在65~70分钟之间,
∴选择全球通较为省钱,
故答案为:全球通.
点评 本题主要考查列代数式的能力及不等式的应用,根据题意表示出两种方案下的总费用是解题的根本和前提,由哪种方案较为省钱分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0.101 001 000 1 | B. | $\frac{13}{17}$ | C. | $0.\stackrel{•}3\stackrel{•}8$ | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+2y=1 | B. | 2y+$\frac{y}{2}$+1=0 | C. | $\frac{2}{x}$+3=0 | D. | 2y2=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
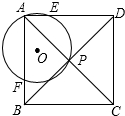 如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.若⊙O的半径为$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,则$\frac{AE}{ED}$的值为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.若⊙O的半径为$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,则$\frac{AE}{ED}$的值为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

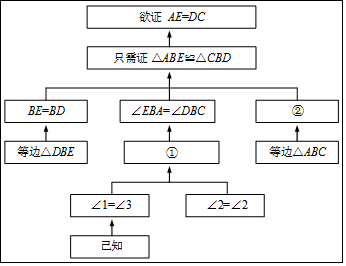
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com