
【题目】问题情境:综合实践活动课上,同学们围绕“已知三角形三边的长度,求三角形的面积”开展活动,启航小组同学想到借助正方形网格解决问题
问题解决:图(1)、图(2)都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,操作发现,启航小组同学在图(1)中画出△ABC,其顶点A,B,C都在格点上,同时构造长方形CDEF,使它的顶点都在格点上,且它的边EF经过点A,ED经过点B.同学们借助此图求出了△ABC的面积.
(1)在图(1)中,△ABC的三边长分别是AB= ,BC= ,AC= .△ABC的面积是 .
(2)已知△PMN中,PM=![]() ,MN=2
,MN=2![]() ,NP=
,NP=![]() .请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .
.请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:

①作∠BAC的平分线AM交BC于点D;
②作边AB的垂直平分线EF,EF与AM相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(1)线段PA,PB,PC之间的数量关系是 ;
(2)若∠ABC=70°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
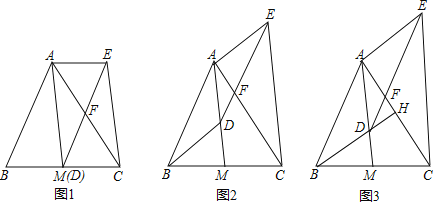
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=![]() , DM=4时,求DH的长.
, DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,延长BC到D,∠ABC和∠ACD的平分线相交于P.
(1)若∠A=60°,则∠P= .
(2)请你用数学表达式归纳出∠P与∠A的关系: .
(3)请说明你的结论(2)正确的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com